
【题目】已知抛物线![]() 经过
经过![]() 两点.
两点.
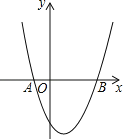
(1)求抛物线的解析式和顶点坐标;
(2)设点![]() 为抛物线上一点,若
为抛物线上一点,若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)抛物线的解析式为![]() ,顶点坐标为
,顶点坐标为![]() (2)
(2)![]() 点坐标为
点坐标为![]() ,
,![]()
【解析】试题分析:(1)由点A、B的坐标利用待定系数法即可求出抛物线的解析式,再利用配方法即可求出抛物线顶点坐标;
(2)设P(x,y),根据三角形的面积公式以及S△PAB=6,即可算出y的值,代入抛物线解析式即可得出点P的坐标.
试题解析:
解:(1)把A(-1,0)、B(3,0)分别代入y=x2+bx+c中,
得: ![]() ,
,
解得: ![]() ,
,
∴抛物线的解析式为y=x2-2x-3.
∵y= x2-2x-3=(x-1)2-4,
∴顶点坐标为(1,-4).
(2)∵A(-1,0)、B(3,0),∴AB=4.
设P(x,y),则S△PAB=![]() AB|y|=2|y|=6,
AB|y|=2|y|=6,
∴|y|=3,
∴y=±3.
①当y=3时,x2-2x-3=3,解得:x1=1+![]() ,x2=1-
,x2=1-![]() ,
,
此时P点坐标为(1+![]() ,3)或(1-
,3)或(1-![]() ,3);
,3);
②当y=-3时,x2-2x-3=-3,解得:x1=0,x2=2,
此时P点坐标为(0,-3)或(2,-3).
综上所述,P点坐标为(1+![]() ,3)或(1-
,3)或(1-![]() ,3)或(0,-3)或(2,-3).
,3)或(0,-3)或(2,-3).


科目:初中数学 来源: 题型:
【题目】图a是一个长为2m、宽为2n的长方形,沿图中实现用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.
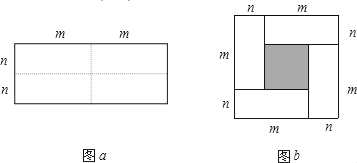
(1)图b中,大正方形的边长是 .阴影部分小正方形的边长是 ;
(2)观察图b,写出(m+n)2,(m﹣n)2,mn之间的一个等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级某班从A、B、C、D四位同学中选出两名同学去参加学校的羽毛球双打比赛.
(1)请用树状图法,求恰好选中A、C两位同学的概率;
(2)若已确定B被选中,再从其余三位同学中随机选取一位,求恰好选中C同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=![]() ,求AF的长.
,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
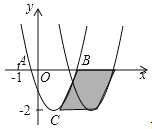
【题目】如图,已知抛物线![]() 与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线
与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线![]() , 则下列结论:① a﹣b+c>0;②b>0;③阴影部分的面积为4;④若c=﹣1,则
, 则下列结论:① a﹣b+c>0;②b>0;③阴影部分的面积为4;④若c=﹣1,则![]() . 其中正确的是__________(写出所有正确结论的序号)
. 其中正确的是__________(写出所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
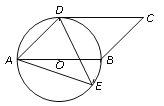
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45.
(1)试判断CD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径为3,sin∠ADE=![]() ,求AE的值.
,求AE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com