
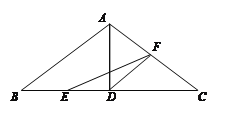
【题目】已知,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、点
、点![]() ,连接
,连接![]() ,若
,若![]() .
.
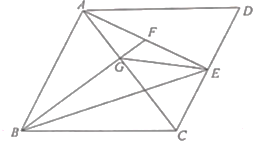
(1)若![]() ,求
,求![]() 的面积.
的面积.
(2)求证:![]() .
.
【答案】(1)72;(2)见解析.
【解析】
(1)由![]() 得AB=CD,AD=BC,AB∥CD,则∠BAG=∠ACE,由
得AB=CD,AD=BC,AB∥CD,则∠BAG=∠ACE,由![]() 得∠ACE+∠EAC=90°,则∠BAG+∠EAC=∠BAE =90°,由
得∠ACE+∠EAC=90°,则∠BAG+∠EAC=∠BAE =90°,由![]() ,
,![]() 可证得∠AFB=∠ACE,又因为BF=BC,
可证得∠AFB=∠ACE,又因为BF=BC,![]() 可得BF=AC,可证△ABF≌△EAC,则AB=AE,
可得BF=AC,可证△ABF≌△EAC,则AB=AE,![]() 的面积=AECD=
的面积=AECD=![]() ,在Rt△ABE中,由BE=12即可求得
,在Rt△ABE中,由BE=12即可求得![]() ;
;
(2)由(1)知:△ABF≌△EAC,得△EAD≌△EAC,设CE=x,则AB=CD=2x,BF=AD=![]() x,根据面积法计算AG的长,作高线GH,利用三角函数分别得EH和GH的长,利用勾股定理计算EG的长,代入结论化简可得结论.
x,根据面积法计算AG的长,作高线GH,利用三角函数分别得EH和GH的长,利用勾股定理计算EG的长,代入结论化简可得结论.
(1)解:∵![]() ,
,
∴AB=CD,AD=BC,AB∥CD,
∴∠BAG=∠ACE,
∵![]() ,
,
∴∠ACE+∠EAC=90°,
∴∠BAG+∠EAC=∠BAE =90°,
∵![]() ,
,![]() ,
,
∴∠AFB=∠ACE,∠AEC =∠BAE =90°,
∵BF=BC,![]() ,
,
∴BF=AC,
∴△ABF≌△EAC,
∴AB=AE,
∴![]() 的面积=AECD=
的面积=AECD=![]() ,
,
在Rt△ABE中, BE=12
∴2![]() =
=![]()
![]() =72,
=72,
∴![]() 的面积=72;
的面积=72;
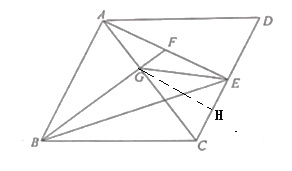
(2)证明:由(1)知:△ABF≌△EAC,
∵BF=BC=AD,
∴△EAD≌△EAC,
∴AF=DE=CE,AE=AB=2CE,
设CE=x,则AB=CD=2x,BF=AD=![]() x,,
x,,
S△ABF=![]() BFAG=
BFAG=![]() AFAB,
AFAB,![]() xAG=x2x,
xAG=x2x,
∴AG=![]() x,
x,
∴CG=![]() x-
x-![]() x=
x=![]() x,
x,
过G作GH⊥CD于H,
sin∠ECG=![]() =
=![]() ,
,
∴GH=![]() x,
x,
cos∠ECG=![]() =
=![]() ,
,
CH=![]() x,
x,
∴EH=x-![]() x=
x=![]() ,
,
∴EG=![]() =
=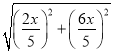 =
=![]() ,
,
∴![]() =
=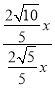 =
=![]() ,
,
∴GE=![]() AG.
AG.
故答案为:(1)72;(2)见解析.


科目:初中数学 来源: 题型:
【题目】我市晶泰星公司安排![]() 名工人生产甲、乙两种产品,每人每天生产
名工人生产甲、乙两种产品,每人每天生产![]() 件甲产品或
件甲产品或![]() 件乙产品.根据市场行情测得,甲产品每件可获利
件乙产品.根据市场行情测得,甲产品每件可获利![]() 元,乙产品每件可获利
元,乙产品每件可获利![]() 元.而实际生产中,生产乙产品需要数外支出一定的费用,经过核算,每生产
元.而实际生产中,生产乙产品需要数外支出一定的费用,经过核算,每生产![]() 件乙产品,当天每件乙产品平均荻利减少
件乙产品,当天每件乙产品平均荻利减少![]() 元,设每天安排
元,设每天安排![]() 人生产乙产品.
人生产乙产品.
(1)根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 |
| ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多![]() 元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级一班和二班各推选![]() 名同学进行投篮比赛,按照比赛规则,每人各投了
名同学进行投篮比赛,按照比赛规则,每人各投了![]() 个球,两个班选手的进球数统计如下表,请根据表中数据回答问题.
个球,两个班选手的进球数统计如下表,请根据表中数据回答问题.
进球数(个) |
|
|
|
|
|
|
一班人数(人) |
|
|
|
|
|
|
二班人数(人) |
|
|
|
|
|
|
![]() 填表;
填表;
平均数 | 中位数 | 众数 | 方差 | |
一班 | 2.6 | |||
二班 | 7 | 7 | 7 |
![]() 如果要从这两个班中选出一个班代表级部参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?
如果要从这两个班中选出一个班代表级部参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC=10cm,BC=16cm,AD⊥BC于D,点E、F分别从B、C两点同时出发,其中点E沿BC向终点C运动,速度为4cm/s;点F沿CA、AB向终点B运动,速度为5cm/s,设它们运动的时间为x(s).
(1)求x为何值时,△EFC和△ACD相似;
(2)是否存在某一时刻,使得△EFD被 AD分得的两部分面积之比为3:5,若存在,求出x的值,若不存在,请说明理由;
(3)若以EF为直径的圆与线段AC只有一个公共点,求出相应x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
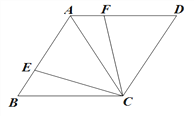
【题目】如图,四边形ABCD中,∠B=60°,对角线AC=BC,点E在AB上,将CE绕点C顺时针旋转60得CF,且点F在AD上.
(1)求证:AF=BE;
(2)若AE=DF,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知过点B(1,0)的直线![]() 与直线
与直线![]() :
:![]() 相交于点P(-1,a).且l1与y轴相交于C点,l2与x轴相交于A点.
相交于点P(-1,a).且l1与y轴相交于C点,l2与x轴相交于A点.
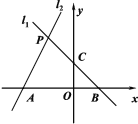
(1)求直线![]() 的解析式;
的解析式;
(2)求四边形![]() 的面积;
的面积;
(3)若点Q是x轴上一动点,连接PQ、CQ,当△QPC周长最小时,求点Q坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EF与AB,CD分别交于点G,H,∠CHG的平分线HM交AB于点M,若∠EGB=50°,则∠GMH的度数为( )
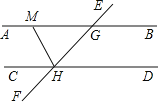
A. 50°B. 55°C. 60°D. 65°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=﹣![]() x+b与x轴、y轴相交于A、B两点,动点C(m,0)在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.
x+b与x轴、y轴相交于A、B两点,动点C(m,0)在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.
(1)求m和b的数量关系;
(2)当m=1时,如图2,将△BCD沿x轴正方向平移得△B′C′D′,当直线B′C′经过点D时,求点B′的坐标及△BCD平移的距离;
(3)在(2)的条件下,直线AB上是否存在一点P,以P、C、D为顶点的三角形是等腰直角三角形?若存在,写出满足条件的P点坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com