Question

如图，已知OC平分∠AOB，D是OC上的任意一点，⊙D与OA相切于点E．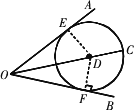

求证：OB与⊙D相切．

Answer 1

答案：
解析：

分析：本题在条件中没有给出直线OB与⊙D有公共点，所以要证OB与⊙D相切，可以先作出点D到OB的垂线段，再证出垂线段的长度等于半径长即可． 　　证明：连接DE． 　　过点D作DF⊥OB，垂足为F． 　　因为OC平分∠AOB，DE⊥OA，DF⊥OB，所以DF＝DE． 　　所以点D到OB的距离等于⊙D的半径． 　　所以OB与⊙D相切． 　　点评：证明直线与圆相切的问题时，一定要分清圆的切线判定定理的条件与结论，特别要注意“经过半径的外端点”和“垂直于这条半径”这两个条件缺一不可．如果题中已有“经过半径的外端点”即“直线与圆有公共点”，只需再证“垂直于这条半径”；如果作出了垂直，只需证明垂线段的长等于半径长．注意不能将点F看成是公共点而连接DF．因此在作辅助线时应注意表述的正确性．