(1)若点(5-a,a-3)在第一、三象限角平分线上,求a的值;
(2)已知两点A(-3,m),B(n,4),若AB∥x轴,求m的值,并确定n的范围;
(3)点P到x轴和y轴的距离分别是3和4,求点P的坐标;
(4)已知点A(x,4-y)与点B(1-y,2x)关于y轴对称,求yx的值.
解:(1)∵点(5-a,a-3)在第一、三象限角平分线上,
∴5-a=a-3,
解得:a=4;
(2)∵两点A(-3,m),B(n,4),AB∥x轴,
∴m=4,n≠3的任意实数;
(3)∵点P到x轴和y轴的距离分别是3和4,
∴P点可能在一、二、三、四象限,
∴点P的坐标为:(4,3),(-4,3),(-4,-3),(4,-3);
(4)∵点A(x,4-y)与点B(1-y,2x)关于y轴对称,
∴
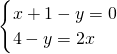
,
解得:
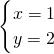
,
∴y
x=2.
分析:(1)根据第一、三象限角平分线上的点横纵坐标相等,即可求出a的值;
(2)根据平行于x轴的直线纵坐标相等求出m的值即可,A,B不应重合得出n的取值范围;
(3)根据P到x轴和y轴的距离分别是3和4,得出P点可能在4个象限,求出即可;
(4)根据关于y轴对称点坐标的性质得出x,y即可.
点评:此题主要考查了点的坐标的变化,熟练掌握各象限内点的坐标符号是解题关键.

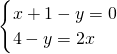 ,
,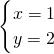 ,
,



 变,问具备什么条件使原结论成立?(要求画出示意图,注明条件,不要求证明)
变,问具备什么条件使原结论成立?(要求画出示意图,注明条件,不要求证明)