
分析 (1)根据不等式的性质可以得到不等式的解集,然后在数轴上表示出来即可;
(2)根据不等式的性质可以得到不等式的解集,然后在数轴上表示出来即可解答本题.
解答 解:(1)-3x+2<2x+3
不等式两边同时减2,得
-3x<2x+1
不等式两边同时减2x,得
-5x<1
两边同时除以-5,得
x>$-\frac{1}{5}$,
故原不等式的解集是x>$-\frac{1}{5}$,在数轴上表示如下所示,
(2)$\frac{1}{3}$x≥$-\frac{2}{3}$x-2
两边同时加$\frac{2x}{3}$,得
x≥-2
故原不等式的解集是x≥-2,在数轴上表示如下所示,
点评 本题考查解一元一次不等式、不等式的性质、在数轴上表示不等式的解集,解题的关键是明确不等式的性质,尤其是两边同时乘或除以一个负数,不等号的方向改变.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
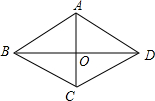 如图,在菱形ABCD中,点O是对角线的交点,|$\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{DO}$|:|$\overrightarrow{CB}+\overrightarrow{CD}+\overrightarrow{AO}$|=$\sqrt{3}$,求菱形ABCD的内角度数.
如图,在菱形ABCD中,点O是对角线的交点,|$\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{DO}$|:|$\overrightarrow{CB}+\overrightarrow{CD}+\overrightarrow{AO}$|=$\sqrt{3}$,求菱形ABCD的内角度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com