练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，将一张矩形纸片ABCD沿着对角线BD向上折叠，顶点C落到点E处，BE交AD于点F．

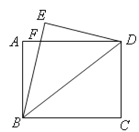
    （1）求证：△BDF是等腰三角形；

    （2）若AB=6，AD=8，求AF的长．

    【答案】（1）见解析；（2）AF=．

    【解析】

    （1）证明△BDF是等腰三角形，可证明BF=DF，可通过证明∠EBD=∠FDB实现，利用折叠的性质和平行线的性质解决；

    （1）设AF=x，则BF=DF=8-x，在Rt△ABF中，利用勾股定理构造方程即可求解．

    （1）根据折叠的性质可得∠DBC=∠DBE，

    ∵AD∥BC，

    ∴∠DBC=∠ADB，

    ∴∠DBE=∠ADB，

    ∴DF=BF，

    ∴△BDF是等腰三角形；

    （2）设AF=x，则BF=DF=8-x，

    在Rt△ABF中，AB2+AF2=BF2，即62+x2=(8﹣x)2，

    解得x=，即AF=．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为了了解学生参加体育活动的情况，学校对学生进行随机抽样调查，其中一个问题是“你平均每天参加体育活动的时间是多少”，共有4个选项：A 1.5小时以上；B 1～1.5小时；C 0.5～1小时；D 0.5小时以下．图1、2是根据调查结果绘制的两幅不完整的统计图，请你根据统计图提供的信息，解答以下问题：

    （1）本次一共调查了多少名学生？

    （2）在图1中将选项B的部分补充完整；

    （3）若该校有3000名学生，你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线与轴的负半轴交于点，与轴交于点，连结，点C(6，)在抛物线上，直线与轴交于点

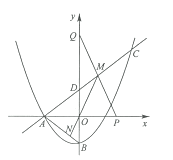
    (1)求的值及直线的函数表达式；

    (2)点在轴正半轴上，点在轴正半轴上，连结与直线交于点，连结并延长交于点，若为的中点．

    ①求证：；

    ②设点的横坐标为，求的长(用含的代数式表示)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB = 90，D为AB的中点，AE∥DC，CE∥DA．

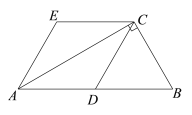
    （1）求证：四边形ADCE是菱形；

    （2）连接DE，若AC =，BC =2，求证：△ADE是等边三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于平面直角坐标系xOy中的定点P和图形F，给出如下定义：若在图形F上存在一点N，使得点Q，点P关于直线ON对称，则称点Q是点P关于图形F的定向对称点．

    （1）如图，，，，

    ①点P关于点B的定向对称点的坐标是 ；

    ②在点，，中，______是点P关于线段AB的定向对称点．

    （2）直线分别与x轴，y轴交于点G，H，⊙M是以点为圆心，为半径的圆．

    ①当时，若⊙M上存在点K，使得它关于线段GH的定向对称点在线段GH上，求的取值范围；

    ②对于，当时，若线段GH上存在点J，使得它关于⊙M的定向对称点在⊙M上，直接写出b的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）计算：；

    （2）尺规作图．如图，已知和线段a，求作，使，，．（不写作法，保留作图痕迹．）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某电器商场销售每台进价分别为200元、170元的A、B两种型号的电风扇，下表是该型号电风扇近两周的销售情况：

    销售时段

    销售数量

    销售收入

    A种型号

    B种型号

    第一周

    3台

    5台

    1800元

    第二周

    4台

    10台

    3100元

    求A、B两种型号的电风扇的销售单价；

    若该商场准备用不多于5400元的金额再采购这两种型号的电风扇共30台，假设售价不变，那么商场应采用哪种采购方案，才能使得当销售完这些风扇后，商场获利最多？最多可获利多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，小明用一张边长为的正三角形硬纸板设计一个无盖的正三棱柱糖果盒，从三个角处分别剪去一个形状大小相同的四边形，其一边长记为，再折成如图2所示的无盖糖果盒，它的容积记为．

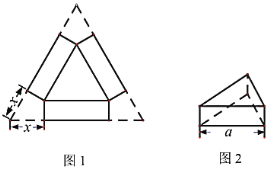
    （1）关于的函数关系式是__________，自变量的取值范围是__________．

    （2）为探究随的变化规律，小明类比二次函数进行了如下探究：

    ①列表：请你补充表格中的数据：

    0

    0．5

    1

    1．5

    2

    2．5

    3

    0

    3．125

    ________

    3．375

    ________

    0．625

    0

    ②描点：请你把上表中各组对应值作为点的坐标，在平面直角坐标系中描出相应的点；

    ③连线：请你用光滑的曲线顺次连接各点．

    （3）利用函数图象解决：

    ①该糖果盒的最大容积是__________；

    ②若该糖果盒的容积超过，请估计糖果盒的底边长的取值范围．（保留一位小数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（阅读理解）

    借助图形的直观性，我们可以直接得到一些有规律的算式的结果，比如：由图①，通过对小黑点的计数，我们可以得到1+2+3+…+n＝n（n+1）；由图②，通过对小圆圈的计数，我们可以得到1+3+5+…+（2n﹣1）＝n2．

    那么13+23+33+…+n3结果等于多少呢？

    如图③，AB是正方形ABCD的一边，BB′＝n，B′B″＝n﹣1，B″B′′′＝n﹣2，……，显然AB＝1+2+3+…+n＝ n（n+1），分别以AB′、AB″、AB′′′、…为边作正方形，将正方形ABCD分割成块，面积分别记为Sn、Sn﹣1、Sn﹣2、…、S1．

    （规律探究）

    结合图形，可以得到Sn＝2BB′×BC﹣BB′2＝　 　，

    同理有Sn﹣1＝　 　，Sn﹣2＝　 　，…，S1＝13．

    所以13+23+33+…+n3＝S四边形ABCD＝　 　．

    （解决问题）

    根据以上发现，计算的结果为　 　．

    查看答案和解析>>

    同步练习册答案