
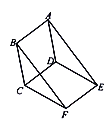
【题目】如图,已知平行四边形ABCD与平行四边形DCFE的周长相等,且![]() BAD=60°,
BAD=60°,![]() CFE=110°,则下列结论:①四边形ABFE为平行四边形;②
CFE=110°,则下列结论:①四边形ABFE为平行四边形;②![]() ADE是等腰三角形;③平行四边形ABCD与平行四边形DCFE全等;④
ADE是等腰三角形;③平行四边形ABCD与平行四边形DCFE全等;④![]() DAE=25°.其中正确的结论是.__________(填正确结论的序号)
DAE=25°.其中正确的结论是.__________(填正确结论的序号)
【答案】①②④.
【解析】
根据平行四边形的对边平行且相等即可证得AB∥CD且AB=CD,则四边形ABFE是平行四边形,根据平行四边形的对边相等以及对角相等即可得到△ADE是等腰三角形,依据等腰三角形的性质即可得证.
∵ABCD中,AB∥CD且AB=CD,
同理CD∥EF且CD=EF.
∴AB∥EF且AB=EF,
∴四边形ABFE是平行四边形.
故①正确;
∵ABCD与DCFE的周长相等,且AB=CD=EF,
∴AD=AE,即△ADE是等腰三角形.
故②正确;
∵∠BAD=60°,平行四边形ABCD中,AB∥CD,
∴∠ADC=180°-∠BAD=180°-60°=120°,
则ABCD与DCFE的角都不相等,故不全等.
故③错误;
∵DCFE中,∠CDE=∠CFE=110°,
∴∠ADE=360°-∠ADC-∠CDE=360°-120°-110°=130°,
又∵AD=DE,
∴∠DAE=![]() =25°.
=25°.
故④正确.
故答案为:①②④.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有38张硬纸板,裁剪时x张用A方法,其余用B方法。
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在![]() 中,
中,![]() 平分
平分![]() (
(![]() ),
),![]() 为
为![]() 上一点,且
上一点,且![]() 于点
于点![]() .
.
(1)当![]() ,
,![]() 时,求
时,求![]() 的度数;
的度数;
(2)若![]() ,
,![]() ,请结合(1)的计算猜想
,请结合(1)的计算猜想![]() 、
、![]() 、
、![]() 之间的数量关系,直接写出答案,不说明理由;(用含有
之间的数量关系,直接写出答案,不说明理由;(用含有![]() 、
、![]() 的式子表示
的式子表示![]() )
)
(3)如图②,当点![]() 在
在![]() 的延长线上时,其余条件不变,则(2)中的结论还成立吗?若成立,请说明为什么;若不成立,请写出成立的结论,并说明为什么.
的延长线上时,其余条件不变,则(2)中的结论还成立吗?若成立,请说明为什么;若不成立,请写出成立的结论,并说明为什么.

查看答案和解析>>
科目:初中数学 来源: 题型:
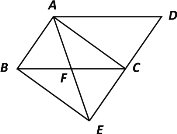
【题目】如图,将□ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
⑴求证:△ABF≌△ECF;⑵若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD对折,使它落在斜边AB上,且与AE重合,则CD等于( )
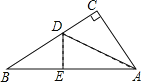
A. 3cmB. 4cmC. 5cmD. 6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明,如图点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.求证:∠FDE=∠A.
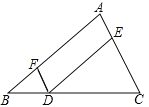
证明:∵DE∥AB,
∴∠FDE=∠ ( )
∵DF∥CA,
∴∠A=∠ ( )
∴∠FDE=∠A( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD;
(2)若∠B=65°,∠EAC=25°,求∠AED的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com