
| A. | 6 | B. | 10 | C. | 12 | D. | 6或10或12 |
分析 根据题意得k≥0且(3$\sqrt{k}$)2-4×8≥0,而整数k<5,则k=4,方程变形为x2-6x+8=0,解得x1=2,x2=4,由于△ABC的边长均满足关于x的方程x2-6x+8=0,所以△ABC的边长可以为2、2、2或4、4、4或4、4、2,然后分别计算三角形周长.
解答 解:根据题意得k≥0且(3$\sqrt{k}$)2-4×8≥0,
解得k≥$\frac{32}{9}$,
∵整数k<5,
∴k=4,
∴方程变形为x2-6x+8=0,解得x1=2,x2=4,
∵△ABC的边长均满足关于x的方程x2-6x+8=0,
∴△ABC的边长为2、2、2或4、4、4或4、4、2.
∴△ABC的周长为6或12或10.
故选D.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了因式分解法解一元二次方程以及三角形三边的关系.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
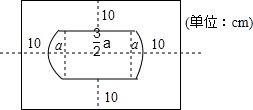 一张餐桌形状如图所示,桌面是由一个长方形和两个半圆组成,一块桌布铺在桌面上,要求桌布垂下部分的宽度都是10cm.
一张餐桌形状如图所示,桌面是由一个长方形和两个半圆组成,一块桌布铺在桌面上,要求桌布垂下部分的宽度都是10cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠ACB=90°,AC=BC,点D、E分别在AB、BC上,且CD=DE,作EF⊥AB于点F.若AD=4,BF=2,求△CDE的面积.
如图,△ABC中,∠ACB=90°,AC=BC,点D、E分别在AB、BC上,且CD=DE,作EF⊥AB于点F.若AD=4,BF=2,求△CDE的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com