
 如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的$\frac{3}{2}$倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大$\frac{3}{2}$倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为(-$\frac{{3}^{n}}{{2}^{n}}$,$\frac{{3}^{n}}{{2}^{n+1}}$).
如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的$\frac{3}{2}$倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大$\frac{3}{2}$倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为(-$\frac{{3}^{n}}{{2}^{n}}$,$\frac{{3}^{n}}{{2}^{n+1}}$). 分析 根据在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k,即可求得Bn的坐标,然后根据矩形的性质即可求得对角线交点的坐标.
解答 解:∵在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的$\frac{3}{2}$倍,
∴矩形A1OC1B1与矩形AOCB是位似图形,点B与点B1是对应点,
∵OA=2,OC=1.
∵点B的坐标为(-2,1),
∴点B1的坐标为(-2×$\frac{3}{2}$,1×$\frac{3}{2}$),
∵将矩形A1OC1B1以原点O为位似中心放大$\frac{3}{2}$倍,得到矩形A2OC2B2…,
∴B2(-2×$\frac{3}{2}$×$\frac{3}{2}$,1×$\frac{3}{2}$×$\frac{3}{2}$),
∴Bn(-2×$\frac{{3}^{n}}{{2}^{n}}$,1×$\frac{{3}^{n}}{{2}^{n}}$),
∵矩形AnOCnBn的对角线交点(-2×$\frac{{3}^{n}}{{2}^{n}}$×$\frac{1}{2}$,1×$\frac{{3}^{n}}{{2}^{n}}$×$\frac{1}{2}$),即(-$\frac{{3}^{n}}{{2}^{n}}$,$\frac{{3}^{n}}{{2}^{n+1}}$),
故答案为:(-$\frac{{3}^{n}}{{2}^{n}}$,$\frac{{3}^{n}}{{2}^{n+1}}$).
点评 本题考查的是矩形的性质、位似变换的性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
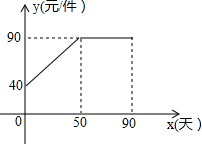 九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元). | 时间x(天) | 1 | 30 | 60 | 90 |
| 每天销售量p(件) | 198 | 140 | 80 | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{3x+y=20}\\{x=y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+3y=20}\\{x=y}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=20}\\{3x=y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=20}\\{x=3y}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
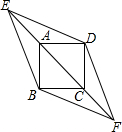 已知边长为4的正方形ABCD,点E、F分别在CA、AC的延长线上,且∠BED=∠BFD=45°,那么四边形EBFD的面积是16+16$\sqrt{2}$.
已知边长为4的正方形ABCD,点E、F分别在CA、AC的延长线上,且∠BED=∠BFD=45°,那么四边形EBFD的面积是16+16$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
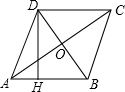 如图,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=8cm,BD=6cm,DH⊥AB于H.
如图,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=8cm,BD=6cm,DH⊥AB于H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com