
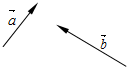
 ��ͼ����֪������ƽ�е�����$\overrightarrow{a}$��$\overrightarrow{b}$���Ȼ�������������4$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$��-2��$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$������Ҫ��д��������Ҫָ��ͼ�б�ʾ���۵�������
��ͼ����֪������ƽ�е�����$\overrightarrow{a}$��$\overrightarrow{b}$���Ȼ�������������4$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$��-2��$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$������Ҫ��д��������Ҫָ��ͼ�б�ʾ���۵������� ���� ֱ������ƽ�������ļӼ����㷨����⼴����ô𰸣����������η��ɻ�������������
���  �⣺ԭʽ=4$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$-2$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$=2$\overrightarrow{a}$-$\overrightarrow{b}$��
�⣺ԭʽ=4$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$-2$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$=2$\overrightarrow{a}$-$\overrightarrow{b}$��
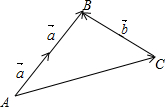
��ͼ��$\overrightarrow{AB}$=2$\overrightarrow{a}$��$\overrightarrow{CB}$=$\overrightarrow{b}$��
��$\overrightarrow{AC}$=2$\overrightarrow{a}$-$\overrightarrow{b}$��
���� ���⿼����ƽ�����������㣮ע��ȥ����ʱ�ķ��ű仯��ע�⻭ͼʱ�������η����Ӧ�ã�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
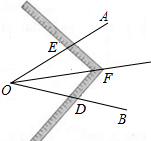 ����ʦ���������ýdz�ƽ��һ������ǣ���ͼ��ʾ����AOB��һ������ǣ��ڱ�OA��OB�Ϸֱ�ȡOD=OE���ƶ��dzߣ�ʹ�dz�������ͬ�Ŀ̶ȷֱ���D��E�غϣ���ʱ���dz߶���P������OP���ǡ�AOB��ƽ���ߣ�����Ϊ����ʦ���ڴ˹������õ���������ȫ�ȵ��ж����������������ĵ����ǣ�������
����ʦ���������ýdz�ƽ��һ������ǣ���ͼ��ʾ����AOB��һ������ǣ��ڱ�OA��OB�Ϸֱ�ȡOD=OE���ƶ��dzߣ�ʹ�dz�������ͬ�Ŀ̶ȷֱ���D��E�غϣ���ʱ���dz߶���P������OP���ǡ�AOB��ƽ���ߣ�����Ϊ����ʦ���ڴ˹������õ���������ȫ�ȵ��ж����������������ĵ����ǣ�������| A�� | SAS | B�� | ASA | C�� | AAS | D�� | SSS |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com