
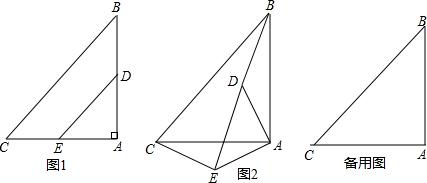
 ;(3)
;(3) .
. ,进而利用弧长公式求出即可.
,进而利用弧长公式求出即可. .
. .
.
 BC=
BC= .
. .
.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源:不详 题型:解答题
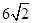 ,∠F=90°,∠EDF=30°, EF=2.将△DEF的斜边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).
,∠F=90°,∠EDF=30°, EF=2.将△DEF的斜边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合). 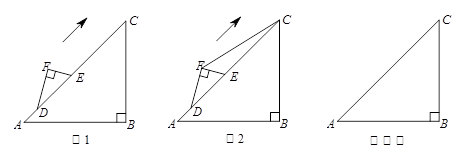
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
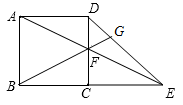
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.有三个直角三角形 |
| B.∠1=∠2 |
| C.∠1和∠B都是∠A的余角 |
| D.∠2=∠A |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
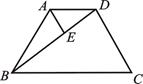
| A.21 | B.18 | C.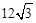 | D.10 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
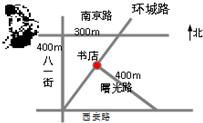
| A.600m | B.500m | C.400m | D.300m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com