
����Ŀ����ͼ1����ABC�У�CD��AB��D����BD=4��AD=6��CD=8��
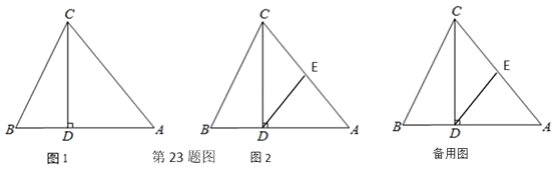
��1����֤����ACB=��ABC��
��2����ͼ2��EΪAC���е㣬����DE������M�ӵ�B������ÿ��1cm���ٶ����߶�BA���A �˶���ͬʱ����N�ӵ�A��������ͬ�ٶ����߶�AC���C�˶���������һ�㵽���յ�ʱ��һ����Ҳֹͣ�˶������M�˶���ʱ��Ϊt���룩��
����MN��BCƽ�У���t��ֵ��
�����ڵ�M�˶��Ĺ����У���MDE�ܷ��Ϊ���������Σ����ܣ����t��ֵ�������ܣ���˵�����ɣ�
���𰸡���1������������2����t=5����tֵΪ9��10�� ![]()
��������
��1�������AB�ij��������ù��ɶ������AC�ij�����AB=AC���ȱ߶ԵȽǼ��ɵó���ACB=��ABC����2���� ������֪AB=AC����˵�AM=ANʱ�� MN��BC �����ǽ��·�̵Ĺ�ϵ�з��̣����t���ɣ�����ΪBD<DE����M��BD��ʱ����BDE�����ܹ��ɵ��������Σ���M��DA��ʱ������������ֱ���⣬��DE=DM����t-4=5�����t���ɣ������ED=EM����M�պ��˶�����A�� ��Ȼt=10�� ���MD=ME����E��EH��AD����EH��HM�ֱ��ú�t�Ĵ���ʽ��ʾ���ڡ�EHM�У������ù��ɶ�����ʽ���t���ɣ�
�⣺
��1��֤������AB=AD+BD=6+4=10��
AC=![]() ��
��
��AB=AC��
�� ��ACB=��ABC.
��2���⣺��ͼ��
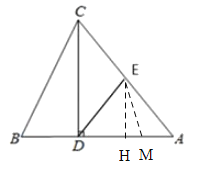
���������BM=t��AN=t����AM=10-t��
��MN��BCʱ��AM=AN��
��10��t=t��
��t=5��
�ڵ���M��DA�ϣ���4��t��10ʱ����MDEΪ���������Σ���3�ֿ��ܣ�
��CD��AB��
���CDA=90�㣬
��EΪAC�е㣬
��DE=![]() AC=5��
AC=5��
���DE=DM����t��4=5��
��t=9��
���ED=EM�����M�˶�����A��
��t=10��
���MD=ME=t��4����E��EH��AD��
��EH��AD��CD��AD��
��EH��CD��
��EΪAC�е㣬
��AE=![]() CD=4��
CD=4��
��![]() ��
�У�
DH=![]() ��
��
��HM=DM-DH=t-4-3=t-7��
����EHM��
��t��4��2����t��7��2=42��
��t= ![]() ��
��
��������������Ҫ���tֵΪ9��10�� ![]() ��
��


 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д� ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�������Σ�BE��EF��DF��EF��BE��2.5cm��DF��4cm����ôEF�ij�Ϊ�� ��
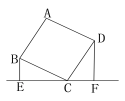
A. 6.5cm B. 6cm C. 5.5cm D. 4cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ����
��ͼ1����֪��ABCΪ�ȱ������Σ���D��E�ֱ��ڱ�AB��AC�ϣ�AD=AE������DC����M��P��N�ֱ�ΪDE��DC��BC���е㣮
��1���۲��������ͼ1�У��߶�PM��PN��������ϵ���� ������MPN�Ķ������� ����
��2��̽��֤�����ѡ�ADE�Ƶ�A��ʱ�뷽����ת��ͼ2��λ�ã�
���жϡ�PMN����״����˵�����ɣ�
�����MPN�Ķ�����
��3����չ����������ABCΪֱ�������Σ���BAC=90�㣬AB=AC=10����DE�ֱ��ڱ�AB��AC�ϣ�AD=AE=4������DC����M��P��N�ֱ�ΪDE��DC��BC���е㣮�ѡ�ADE�Ƶ�A��ƽ����������ת����ͼ3����ֱ��д����PMN��������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ĵ����������ɸ�С�����dz�����ɫ�⣬��������ͬ����ͬѧ�Ӵ������������һ��������ɫ��Żش����ҡ�Ⱥ��ٴ��������һ��������ɫ��������ͬѧ��������ʵ����ݰ�����ֵ�Ƶ�ʻ�������ͼ��ʾ��ͳ��ͼ��������˵����ȷ���ǣ�������

A. ����һ������������
B. �����а���ռС��������ʮ��֮��
C. ����������һ����һ���ǰ���
D. ����1000�Σ���������Ĵ�����ӽ�330��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ƶ��������У�������ѧ�ƻ�ѡ���ס���������Ʒο��ƶ��������֪����Ʒ�ĵ��۱�����Ʒ�ĵ��۸�10Ԫ������500Ԫ�����������Ʒ��450Ԫ������������Ʒ��������ͬ��
��1�����ʼס���������Ʒ�ĵ��۸�Ϊ���٣�
��2������õ�λ�ƻ�����ס���������Ʒ��55�����ܷ��ò�����5000Ԫ�Ҳ�����5020Ԫ��ͨ������ó����м���ѡ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�ϡ�С��������İ���˼ס���ͬ����ͼ��ʾ�ĵ��³���ȵ���,��֪����İ���˵�1��4�������һ��¥������.
![]()
(1)���б�����״ͼ����ס���������ͬһ��¥�����ݵĸ���;
(2)С�Ϻ�С������,������:���ס�����ͬһ�������¥�������,��С��ʤ,����С��ʤ.����Ϸ�Ƿ�ƽ?����ƽ,˵������;������ƽ,������Ϸ����,ʹ��Ϸ��ƽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�E��F�ǶԽ���BD�����㣬�ҡ�EAF=45��������ADF�Ƶ�A˳ʱ����ת90���õ���ABQ������EQ����֤��
��1��EA�ǡ�QED��ƽ���ߣ�
��2��EF2=BE2+DF2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������������У�ÿ��С����ı߳���Ϊ1����![]() �����㶼�ڸ���ϣ�����
�����㶼�ڸ���ϣ�����![]() ������Ϊ��0��3�����밴Ҫ�����������⣺
������Ϊ��0��3�����밴Ҫ�����������⣺
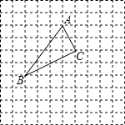
��1����ͼ�н�������������ƽ��ֱ������ϵ��
��2������������������ϵ��д����![]() �͵�
�͵�![]() �����ꣻ
�����ꣻ
��3��������![]() ����
����![]() ��ĶԳ�ͼ�Ρ�
��ĶԳ�ͼ�Ρ�![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���ACB=90�㣬AC=6cm��BC=8cm������P�ӵ�B��������BA������ÿ��5cm���ٶ����A�����˶���ͬʱ����Q�ӵ�C��������CB������ÿ��4cm���ٶ����B�����˶����˶�ʱ��Ϊt�루0��t��2��������PQ��

��1������BPQ����ABC���ƣ���t��ֵ��
��2������AQ��CP����AQ��CP����t��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com