
【题目】在平面内,对于给定的![]() ,如果存在一个半圆或优弧与
,如果存在一个半圆或优弧与![]() 的两边相切,且该弧上的所有点都在
的两边相切,且该弧上的所有点都在![]() 的内部或边上,则称这样的弧为
的内部或边上,则称这样的弧为![]() 的内切弧.当内切弧的半径最大时,称该内切弧为
的内切弧.当内切弧的半径最大时,称该内切弧为![]() 的完美内切弧.(注:弧的半径指该弧所在圆的半径)
的完美内切弧.(注:弧的半径指该弧所在圆的半径)
在平面直角坐标系![]() 中,
中,![]() .
.
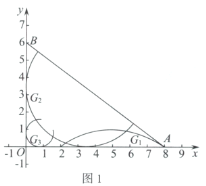
(1)如图1,在弧![]() ,弧
,弧![]() ,弧
,弧![]() 中,是
中,是![]() 的内切弧的是____________;
的内切弧的是____________;
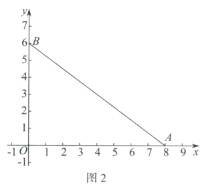
(2)如图2,若弧G为![]() 的内切弧,且弧G与边
的内切弧,且弧G与边![]() 相切,求弧G的半径的最大值;
相切,求弧G的半径的最大值;
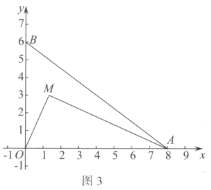
(3)如图3,动点![]() ,连接
,连接![]() .
.
①直接写出![]() 的完美内切弧的半径的最大值;
的完美内切弧的半径的最大值;
②记①中得到的半径最大时的完美内切弧为弧T.点P为弧T上的一个动点,过点P作x轴的垂线,分别交x轴和直线![]() 于点D,E,点F为线段
于点D,E,点F为线段![]() 的中点,直接写出线段
的中点,直接写出线段![]() 长度的取值范围.
长度的取值范围.
【答案】(1)弧![]() ,弧
,弧![]() .(2)3. (3)①
.(2)3. (3)①![]() . ②
. ②![]() 且
且![]() .
.
【解析】
(1)根据内切弧定义即可解答;
(2)由内切弧定义可知弧G所在圆的圆心上![]() 的角平分线
的角平分线![]() 上,弧G的半径最大时其圆心I在
上,弧G的半径最大时其圆心I在![]() 的边
的边![]() 上.再由勾股定理即可计算出半径最大值;
上.再由勾股定理即可计算出半径最大值;
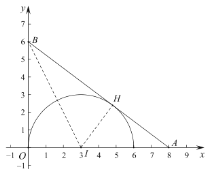
解:(1)由图可知,弧![]() 是半圆,弧
是半圆,弧![]() 是优弧,它们与
是优弧,它们与![]() 的两边相切,且该弧上的所有点都在
的两边相切,且该弧上的所有点都在![]() 的内部或边上,故弧
的内部或边上,故弧![]() ,弧
,弧![]() 是
是![]() 的内切弧;而弧
的内切弧;而弧![]() 只与一边相切,而且是劣弧,故弧
只与一边相切,而且是劣弧,故弧![]() 不是
不是![]() 的内切弧;,
的内切弧;,
弧![]() ,弧
,弧![]() .
.
(2)∵弧G为![]() 的内切弧,且弧G与边
的内切弧,且弧G与边![]() 相切,
相切,
∴弧G所在圆的圆心上![]() 的角平分线
的角平分线![]() 上.
上.
易知若弧G的半径最大,则弧G所在圆的圆心I在![]() 的边
的边![]() 上.设弧G与边
上.设弧G与边![]() 相切分别切于点O,H.
相切分别切于点O,H.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
在![]() 中,
中,![]() ,即
,即![]() .
.
解得![]() .
.
(3)①![]() 的完美内切弧半径的最大值为
的完美内切弧半径的最大值为![]() .
.
理由如下:由内切弧定义可知,内切弧的圆心在相切两边的夹角的角平分线上,而完美内切弧的圆心在最大内角的角平分线与其对边的交点上,
动点![]() 在
在![]() ,
,
∵![]() ,
,
则有![]() 垂直平分OB,
垂直平分OB,
∴MO=MB,
∴MB+MA=MO+MA.
根据两点之间线段最短可得:当B、M、A三点共线时,即M点在AB的中点(4,3),MO+MA取到最小值,最小值为AB长=10.
I.当内切弧与OM、MA相切时,如图: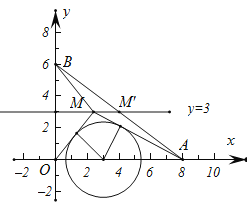
设![]() 的完美内切弧半径为r,
的完美内切弧半径为r,
∵![]() ,
,
∴![]()
∴![]() .
.
当MO+MA取最小值10时,此时r取到最大值,最大值为![]() .
.
II.当完美内切弧与OM、OA相切时,或与MA、OA相切时,相切两边的和为:![]() ,
,![]() ,
,
同理可知,这两种情况的内切弧的半径最大值小于完美内切弧与OM、MA相切时的半径.
综上所述:![]() 的完美内切弧是内切弧与OM、MA相切时的半径的最大值为
的完美内切弧是内切弧与OM、MA相切时的半径的最大值为![]()
②线段![]() 长度的取值范围是
长度的取值范围是![]() 且
且![]() .
.
由①可知:![]() 的完美内切弧的圆心O坐标为(4,0),半径为
的完美内切弧的圆心O坐标为(4,0),半径为![]() ,
,
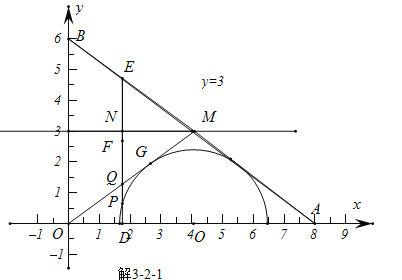
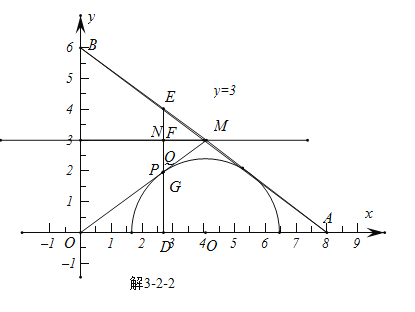
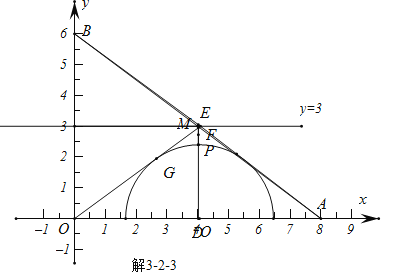

由图解3-2-1,解3-2-2,解3-2-3,解3-2-4,可知,当DE经过切点Q的时候,DF最大为3;
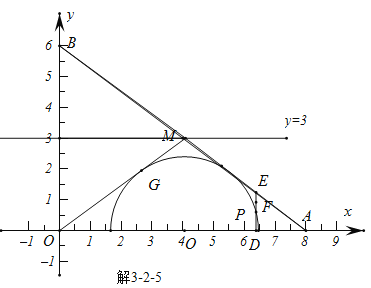
由图解3-2-5可知,当DE与半圆右侧相切的时候,DF最小为![]() ;
;
而当ED经过AB与半圆相切的切点时,此时F点不存在,DF=![]() ,
,
∴线段![]() 长度的取值范围是
长度的取值范围是![]() 且
且![]() .
.


科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)经过点D(2,4),与x轴交于A,B两点,与y轴交于点C(0,4),连接AC,CD,BC, 其且AC=5.
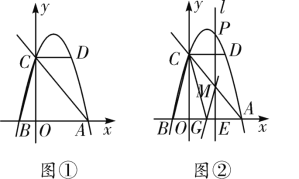
(1)求抛物线的解析式;
(2)如图②,点P是抛物线上的一个动点,过点P作x轴的垂线l,l分别交x轴于点E,交直线AC于点M.设点P的横坐标为m.当0<m≤2时,过点M作MG∥BC,MG交x轴于点G,连接GC,则m为何值时,△GMC的面积取得最大值,并求出这个最大值;
(3)当-1<m≤2时,是否存在实数m,使得以P,C,M为顶点的三角形和△AEM相似?若存在,求出相应m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P是平面内任意一点,点A,B是![]() 上不重合的两个点,连结
上不重合的两个点,连结![]() .当
.当![]() 时,我们称点P为
时,我们称点P为![]() 的“关于
的“关于![]() 的关联点”.
的关联点”.

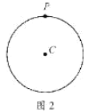
(1)如图2,当点P在![]() 上时,点P是
上时,点P是![]() 的“关于
的“关于![]() 的关联点”时,画出一个满足条件的
的关联点”时,画出一个满足条件的![]() ,并直接写出
,并直接写出![]() 的度数;
的度数;
(2)在平面直角坐标系中有点![]() ,点M关于y轴的对称点为点N.
,点M关于y轴的对称点为点N.
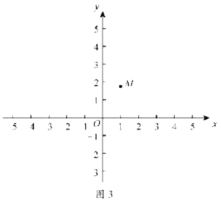
①以点O为圆心,![]() 为半径画
为半径画![]() ,在y轴上存在一点P,使点P为
,在y轴上存在一点P,使点P为![]() “关于
“关于![]() 的关联点”,直接写出点P的坐标;
的关联点”,直接写出点P的坐标;
②点![]() 是x轴上一动点,当
是x轴上一动点,当![]() 的半径为1时,线段
的半径为1时,线段![]() 上至少存在一点是
上至少存在一点是![]() 的“关于某两个点的关联点”,求m的取值范围.
的“关于某两个点的关联点”,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坚持节约资源和保护环境是我国的基本国策,国家要求加强生活垃圾分类回收与再生资源回收有效衔接,提高全社会资源产出率,构建全社会的资源循环利用体系.
图1反映了2014—2019年我国生活垃圾清运量的情况.

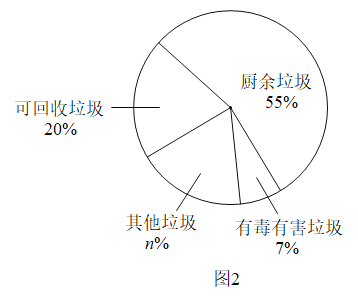
图2反映了2019年我国G市生活垃圾分类的情况.
根据以上材料回答下列问题:
(1)图2中,n的值为___________;
(2)2014—2019年,我国生活垃圾清运量的中位数是_________;
(3)据统计,2019年G市清运的生活垃圾中可回收垃圾约为0.02亿吨,所创造的经济总价值约为40亿元.若2019年我国生活垃圾清运量中,可回收垃圾的占比与G市的占比相同,根据G市的数据估计2019年我国可回收垃圾所创造的经济总价值是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
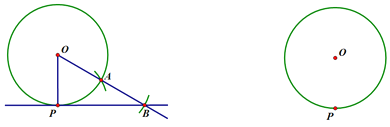
【题目】已知⊙O及⊙O上一点P,过点P作⊙O的切线.
小明设计了如下尺规作法:
①连接OP,以点P为圆心,OP长为半径画弧交⊙O于点A;
②连接OA,延长OA到B,使AB=OA,作直线PB.则直线即为所求作.
(1)请证明小明作法的正确性;
(2)请你自己再设计一种尺规作图方法(保留痕迹,不要证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在趣味运动会“定点投篮”项目中,我校七年级八个班的投篮成绩![]() 单位:个
单位:个![]() 分别为:24,20,19,20,22,23,20,
分别为:24,20,19,20,22,23,20,![]() 则这组数据中的众数和中位数分别是
则这组数据中的众数和中位数分别是![]()
![]()
A. 22个、20个 B. 22个、21个 C. 20个、21个 D. 20个、22个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD内部有若干个点,则用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
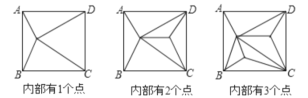
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | ... | n |
分割成三角形的个数 | 4 | 6 | _____ | _____ | ... | _____ |
(2)原正方形能否被分割成2021个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
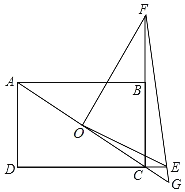
【题目】如图,在矩形ABCD中,AB=9,AD=6,点O为对角线AC的中点,点E在DC的延长线上且CE=1.5,连接OE,过点O作OF⊥OE交CB延长线于点F,连接FE并延长交AC的延长线于点G,则![]() =_____.
=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com