
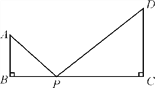
【题目】如图,已知AB⊥BC于点B,CD⊥BC于点C,AB=4,CD=6,BC=14,P为BC边上一点,试问BP为何值时,以A,B,P为顶点的三角形与以P,C,D为顶点的三角形相似?
科目:初中数学 来源: 题型:
【题目】如图是某学校高中两个班的学生上学时步行、骑车、乘公交、乘私家车人数的扇形统计图,已知乘公交人数是乘私家车人数的2倍.若步行人数是18人,则下列结论正确的是( )

A. 被调查的学生人数为90人
B. 乘私家车的学生人数为9人
C. 乘公交车的学生人数为20人
D. 骑车的学生人数为16人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场出售一批进价为2元的贺卡,在市场营销中发现商品的日销售单价x元与日销售量y个之间有如下关系:
x(元/个) | 3 | 4 | 5 | 6 |
y(个) | 20 | 15 | 12 | 10 |
(1)根据表中数据,在直角坐标系描出实数对(x,y)的对应点
(2)猜测并确定y与x之间的函数关系式,并画出图象;
(3)设经营此贺卡的销售利润为W元,试求出W与x之间的函数关系式,若物价局规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价x定为多少元时,才能获得最大日销售利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC:y=x交于点C.
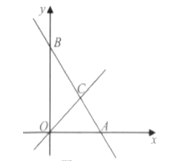
(1)若直线AB解析式为![]() .
.
①求点C的坐标;
②根据图象,求关于x的不等式0<-![]() x+10<x的解集;
x+10<x的解集;
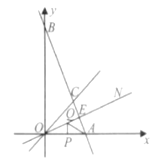
(2)如下图,作∠AOC的平分线ON,若AB⊥ON,垂足为E,ΔOAC的面积为9,且OA=6,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值:若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图, 请根据图中提供的信息,完成下列问题:
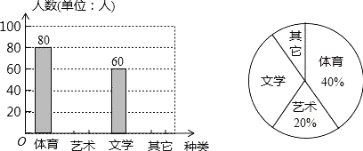
(1)此次共调查了 人;
(2)求文学社团在扇形统计图中所占圆心角为 度;
(3)请将条形统计图补充完整;
(4)若该校有 1500 名学生,请估计喜欢体育类社团的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测倾器测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.则河的宽度为________米(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
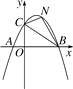
【题目】如图,抛物线y=-![]() [(x-2)2+n]与x轴交于点A(m-2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连接BC.
[(x-2)2+n]与x轴交于点A(m-2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连接BC.
(1)求m,n的值;
(2)点N为抛物线上的一动点,且位于直线BC上方,连接CN,BN.求△NBC面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线DB于点F,AF交⊙O于点H,连结BH.
(1)求证:AC=CD;
(2)若OB=2,求BH的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com