
����Ŀ���Ķ��������
������һ����һ��˳�����е�һ������Ϊ���У�������{an}��n�������������������е�ÿһ����������������е�����ڵ�һλ������Ϊ������еĵ�l��
��ͨ��Ҳ���������������al�����ڵڶ�λ������Ϊ������еĵ�2�������a2���������ڵڴ�λ������Ϊ������еĵ�n�������an ��
�����϶������һ�����дӵڶ�����ÿһ��������ǰһ��IJ����ͬһ��������������оͽ����Ȳ����У�������������Ȳ����еĹ���������ĸd��ʾ��
���磺����l0��l5��20��25�ǵȲ����У�
�������al �� a2 �� a3 �� ����an �� ���ǵȲ����У���ôa2��al=d��a3��a2=d������
an��an��l=d������a2=al+d��a3=a2+d=al+d+d=al+2d��a4=a3+d=al+3d������
�����������ϣ��������
��1�������������ڵȲ����е��� ��ֻ����ţ���
��l��2��3��4��5����2��4��6��8��10��11����l��1��1��1��1��
��2����֪����{an}�ǵȲ����У�
��al=1��a2=4��a3=7��������al0= ��
������a1=23������d=2����an= ��
��3����֪�Ȳ�����{an}����a2=0��a6+a8=��10����an ��
���𰸡�
��1���٢�
��2��28��2n+21
��3��
�⣺�ߵȲ�����{an}��������a1��������d��
�� ![]()
��ã�a1=1��d=��1��
��an=1+��n��1��������1��=��n+2��
���������⣺��1���ڢ��к����������ǰ�������1�����ǵȲ����У�
�ڢ���ǰ�����ÿ���ڵ��������IJ�Ϊ2�����������͵�����IJ�ֵ��1���ʲ��ǵȲ����У�
�ڢ��У������������ǰ������IJ�ֵ����0�����ǵȲ����У�
���Դ��ǣ��٢ۣ�
2���١�����{an}�ǵȲ����У�a2��a1=4��1=3=d��
��a10=1+��10��1����3=1+9��3=28��
�ڡ�����{an}�ǵȲ����У�����a1=23������d=2��
��an=23+��n��1����2=2n+21��
���Դ��ǣ���28����2n+21��
�����㾫�������ڱ��⿼��������������������㣬��Ҫ�˽���û�����ŵIJ�ͬ�������У�����˷�����˳��������Ӽ����ܵó���ȷ�𰸣�


 �����߿����ϵ�д�
�����߿����ϵ�д� �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д� Сѧ�̲���ȫ���ϵ�д�
Сѧ�̲���ȫ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ��չ������μ�����Ҫ�����������������ɸ�����֪����2�������3��������Ҫ380Ԫ������4�������5��������Ҫ700Ԫ��
(1)����һ������һ������������Ԫ��
(2)��������ʦ����8000Ԫȥ������������������100�������������϶࣬����������һ�ɴ���ۡ����Żݼۣ���ô������ܹ�����ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�����������ĸ����ۣ���abc=0����a+b+c��0����a��b����b2��4ac��0��������ȷ�Ľ����У� �� 
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������ABCD������������ȱ�������ADE��DCF������AF��BE��

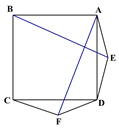

��ͼ1�� ��ͼ2�� ������ͼ��
��1�����жϣ�AF��BE��������ϵ��_____________��λ�ù�ϵ______________��
��2����ͼ2�����������������ȱ�������ADE��DCF����Ϊ����������������ADE��DCF����EA=ED=FD=FC�����ڣ�1�����еĽ����Ƿ���Ȼ�������������жϲ�����֤����
��3����������ADE��DCFΪһ�������Σ���AE=DF��ED=FC���ڣ�1�����еĽ��۶��ܳ�������ֱ��д������жϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�죬С����С��һ���濨Ƭ��Ϸ�����Ƿֱ�������������ֱ������ĸA��B��C���IJ�����Ƭ����ϷԼ����ÿ�˽����ԵĿ�Ƭ���泯��Ūϴ���ȣ�Ȼ�������ȡһ�ţ����ſ�Ƭ�У����ͬΪԪ��������ĸ����Ϊƽ�֣����һ��Ԫ����ĸһ��������ĸ����鵽Ԫ����ĸ��ʤ��
��1�������б�����״ͼ�ķ����оٳ����г��ֽ���Ŀ����ԣ�
��2����С����ʤ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У���ABD��ƽ����BE��AD�ڵ�E����CDB��ƽ����DF��BC�ڵ�F����֤���ı���DEBF��ƽ���ı��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����CAD�͡�CBD��ƽ�����ཻ�ڵ�P�����CAD����CBD����C����D�Ķ�������Ϊa��b��c��d���ý�������2����ĸ�Ĵ���ʽ����ʾ��P�Ķ�����_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ʵ��ķ���������ķ���
��3x2+x��1=0
�ڣ�3x��2��2=4��3��x��2 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���洬��B����õ���A�ڱ�ƫ��60���ķ�����һ�һ�����C����õ���A�ڱ�ƫ��40���ķ�����ô�ڵ���A���ۿ�B��Cʱ���ӽǡ�BAC�Ƕ��ٶȣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com