Question

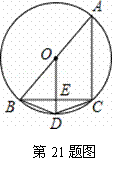
如图，圆内接四边形ABDC，AB是⊙O的直径，OD⊥BC于E．

（1）求证：∠BCD=∠CBD；

（2）若BE=4，AC=6，求DE的长．

 

Answer 1

解：（1）证明：∵OD⊥BC于E

         ∴=                     ………………2分

         ∴∠BCD=∠CBD                      ………………4分

                                                

（2）解法一：

∵OD⊥BC，BE=4，∴BE=CE=4，即BC=2BE=8。………6分

∵AB为圆O的直径，∴∠ACB=90°。

在Rt△ABC中，AC=6，BC=8，根据勾股定理得：AB=10。………7分

∴OB=5。………8分

在Rt△OBE中，OB=5，BE=4，根据勾股定理得：OE=3。………10分

∴ED=OD﹣OE=5﹣3=2。  ………12分

解法二：

∵AB为圆O的直径，∴∠ACB=90°

∵OD⊥BC， ∴OE∥AC                 ………6分

∵ 点O是AB的中点，∴OE是△ABC的中位线

∴OE=AC=3                          ………8分

在Rt△OBE中，OE=3，BE=4，根据勾股定理得：OB=5。即：OD=5

                                     ………10分

∴ED=OD﹣OE=5﹣3=2。                ………12分