
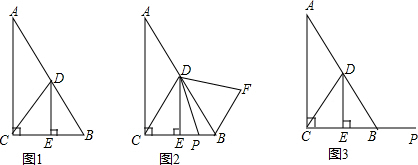
���� ��1�����BE=CE����ֱ�����������BE���ɣ�
��2�����DC=DB����CDB=60�㣬������ת�����PDF=60�㣬DP=DF�������CDP=��BDF������SAS�Ƴ���DCP�ա�DBF������ȫ���������CP=BF����ֱ�����������CE=$\frac{{\sqrt{3}}}{3}$DE���ɣ�
��3����P���߶�BC��ʱ��BF+BP=2DEtan������P��BC�ӳ�����ʱ��BF-BP=2DEtan��������ͼ1�����DC=DB=AD��DE��AC���Ƴ���A=��ACD=������EDB=��A=����BC=2CE������ȫ�������ε��ж��Ƴ���DCP�ա�DBF������ȫ�ȵ����ʵó�CP=BF�����BF+BP=BC����ֱ�����������CE=DEtan�����ɣ�
����ͼ2�����DC=DB=AD��DE��AC�������FDB=��CDP=2��+��PDB��DP=DF������ȫ�������ε��ж��ó���DCP�ա�DBF�����CP=BF���Ƴ�BF-BP=BC����ֱ�����������CE=DEtan�����ɣ�
��� �⣺��1��DE=$\sqrt{3}$EC��
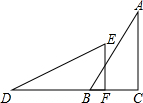
�����ǣ�����Rt��ACB�У���ACB=90�㣬��A=30�㣬
���B=60�㣬
�ߡ�ACB=90�㣬DΪAB���е㣬
��CD=BD��
��DE��BC��
��BE=EC��
��tan60��=$\frac{DE}{BE}$��
��DE=$\sqrt{3}$BE��
��DE=$\sqrt{3}$CE��
�ʴ�Ϊ��DE=$\sqrt{3}$CE��
��2��DE��BF��BP����֮���������ϵ��BF+BP=$\frac{{2\sqrt{3}}}{3}$DE��
�������£�
�ߡ�ACB=90�㣬D��AB���е㣬��A=30��
��DC=DB����CDB=60�㣮
���߶�DP�Ƶ�D��ʱ����ת60��õ��߶�DF��
���PDF=60�㣬DP=DF��
�֡ߡ�CDB=60�㣬���CDB-��PDB=��PDF-��PDB��
���CDP=��BDF��
�ڡ�DCP�͡�DBF��
$\left\{\begin{array}{l}{DC=DB}\\{��CDP=��BDF}\\{DP=DF}\end{array}\right.$
���DCP�ա�DBF��
��CP=BF��
�� CP=BC-BP��
��BF+BP=BC��
��Rt��CDE�У���DEC=90�㣬
��$tan��DCE=\frac{DE}{CE}$��
��CE=$\frac{{\sqrt{3}}}{3}$DE��
��BC=2CE=$\frac{{2\sqrt{3}}}{3}$DE��
��BF+BP=$\frac{{2\sqrt{3}}}{3}$DE��
��3����P���߶�BC��ʱ��BF+BP=2DEtan������P��BC�ӳ�����ʱ��BF-BP=2DEtan����
�����ǣ�����ͼ1��
�ߡ�ACB=90�㣬D��AB���е㣬DE��BC����A=����
��DC=DB=AD��DE��AC��
���A=��ACD=������EDB=��A=����BC=2CE��
���BDC=��A+��ACD=2����
�ߡ�PDF=2����
���FDB=��CDP=2��-��PDB��
���߶�DP�Ƶ�D��ʱ����ת2���õ��߶�DF��
��DP=DF��
�ڡ�DCP�͡�DBF��
$\left\{\begin{array}{l}{DC=DB}\\{��CDP=��BDF}\\{DP=DF}\end{array}\right.$
���DCP�ա�DBF��
��CP=BF��
�� CP=BC-BP��
��BF+BP=BC��
��Rt��CDE�У���DEC=90�㣬
��$tan��DCE=\frac{DE}{CE}$��
��CE=DEtan����
��BC=2CE=2DEtan����
��BF+BP=2DEtan����
�ڵ�P��BC�ӳ�����ʱ��BF-BP=2DEtan����
��ͼ2��
�ߡ�ACB=90�㣬D��AB���е㣬DE��BC����A=����
��DC=DB=AD��DE��AC��
���A=��ACD=������EDB=��A=����BC=2CE��
���BDC=��A+��ACD=2����
�ߡ�PDF=2����
���FDB=��CDP=2��+��PDB��
���߶�DP�Ƶ�D��ʱ����ת2���õ��߶�DF��
��DP=DF��
�ڡ�DCP�͡�DBF��
$\left\{\begin{array}{l}{DC=DB}\\{��CDP=��BDF}\\{DP=DF}\end{array}\right.$
���DCP�ա�DBF��
��CP=BF��
�� CP=BC+BP��
��BF-BP=BC��
��Rt��CDE�У���DEC=90�㣬
��$tan��DCE=\frac{DE}{CE}$��
��CE=DEtan����
��BC=2CE=2DEtan����
��BF-BP=2DEtan����
���� ���⿼����������������ʣ�ȫ�������ε����ʺ��ж���ֱ�������ε����ʣ���ת�����ʵ�Ӧ�ã����Ƴ���DCP�ա�DBF�ǽ����Ĺؼ����ۺ��ԱȽ�ǿ��֤���������ƣ�


 ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���A������Ϊ��5��0��������B��C���ڵ�һ���ޣ��Խ���AC��OB�ཻ�ڵ�D��˫����y=$\frac{k}{x}$��x��0��������D����AC•OB=40����k��ֵΪ8��
��ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���A������Ϊ��5��0��������B��C���ڵ�һ���ޣ��Խ���AC��OB�ཻ�ڵ�D��˫����y=$\frac{k}{x}$��x��0��������D����AC•OB=40����k��ֵΪ8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
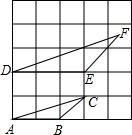 ��ͼ����5��5�������η����У���ABC�͡�DEF�Ķ��㣨����F�����ڱ߳�Ϊ1��С�����εĶ����ϣ���DF��EF��С�����ζ��㣬�����н��۲���ȷ���ǣ�������
��ͼ����5��5�������η����У���ABC�͡�DEF�Ķ��㣨����F�����ڱ߳�Ϊ1��С�����εĶ����ϣ���DF��EF��С�����ζ��㣬�����н��۲���ȷ���ǣ�������| A�� | ��DEF=��ABC | B�� | ��ABC�͡�DEF�������Ϊ3��2 | ||
| C�� | ��ABC�ı�AB�ϵĸ�Ϊ1 | D�� | ��DEF�ı�DE�ϵĸ�Ϊ$\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
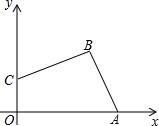 ��ͼ����ƽ��ֱ������ϵ�У���A��4��0����B��3��4����C��0��2��
��ͼ����ƽ��ֱ������ϵ�У���A��4��0����B��3��4����C��0��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
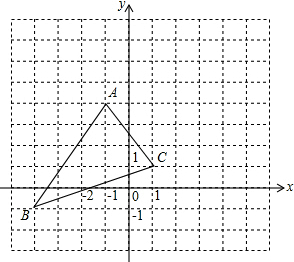
 ��ͼ����ABC�ա�DEF����C=��DFE=90�㣬A��D�� ��Ӧ�㣬Ҫʹ��DEFͨ�����α任���ABC�غϣ������еı任�ǣ�������
��ͼ����ABC�ա�DEF����C=��DFE=90�㣬A��D�� ��Ӧ�㣬Ҫʹ��DEFͨ�����α任���ABC�غϣ������еı任�ǣ�������| A�� | ��Գ� | B�� | ƽ�� | C�� | ��ת | D�� | ���ĶԳ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com