

分析 (1)令x=0代入抛物线可得y=3a,即OA=3a,因为OB=2OA,所以B的坐标为(6a,0),点C时抛物线的顶点,利用顶点坐标公式即可求出C的坐标为(2,-a);
(2)由于点B的位置不确定,所以分三种情况讨论,一是点B在点D的左侧,二是点B在点D的右侧,三是点B与点D重合,其中第三种情况是不存在△BCD与△BDE;另外,△BCD与△BDE相似时,有两种情况,一是∠DBC=∠EBD,二是∠DBE=∠DBC,利用相似三角形的性质即可求出a的值;
(3)由于点B的位置不确定,所以分三种情况讨论,一是点B在点D的左侧,二是点B在点D的右侧,三是点B与点D重合,其中第三种情况是不存在△OBE,由题意知:点M在OB和BE的垂直平分线上,设OB和BE的垂直平分线交于点M,其中OB的垂直平分线与OB交于点G,BE的垂直平分线交OB于点H,交BE于点F,利用相似三角形的性质求出MF的长度即可;
解答 解:(1)由抛物线的解析式可知:点C的坐标为(2,-a),
令x=0代入y=ax2-4ax+3a,
∴y=3a,
∴OA=3a,
∵OB=2OA=6a,
∴点B的坐标为(6a,0);
(2)由(1)可知:OD=2,CD=a,OB=6a,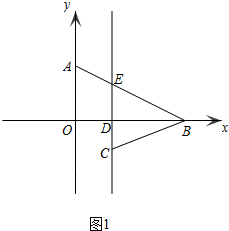
若点B在点D的右侧时,如图1,
则6a>2,
∴a>$\frac{1}{3}$,
∴BD=6a-2,
当∠DBC=∠EBD时,
∴tan∠DBC=tan∠EBD=$\frac{OA}{OB}$=$\frac{1}{2}$,
∴$\frac{CD}{BD}=\frac{1}{2}$,
∴$\frac{a}{6a-2}$=$\frac{1}{2}$,
∴a=$\frac{1}{2}$,
当∠DCB=∠EBD时,
∴tan∠DCB=tan∠EBD=$\frac{1}{2}$,
∴$\frac{BD}{CD}=\frac{1}{2}$,
∴$\frac{6a-2}{a}=\frac{1}{2}$,
∴a=$\frac{4}{11}$,
若点B在点D的左侧时,如图2,
则0<6a<2,
∴0<a<$\frac{1}{3}$,
∴BD=2-6a,
当∠DBC=∠EBD时,
∴tan∠DBC=tan∠EBD=$\frac{OA}{OB}$=$\frac{1}{2}$,
∴$\frac{CD}{BD}=\frac{1}{2}$,
∴$\frac{a}{2-6a}$=$\frac{1}{2}$,
∴a=$\frac{1}{4}$,
当∠DCB=∠EBD时,
∴tan∠DCB=tan∠EBD=$\frac{1}{2}$,
∴$\frac{BD}{CD}=\frac{1}{2}$,
∴$\frac{2-6a}{a}$=$\frac{1}{2}$,
∴a=$\frac{4}{13}$,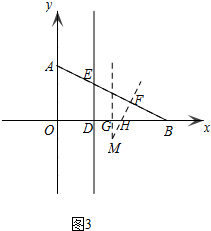
若点B与点D重合时,
则6a=2,
∴a=$\frac{1}{3}$,
此情况不存在△BCD与△BDE,
综上所述,a的值为$\frac{1}{2}$、$\frac{4}{11}$、$\frac{4}{13}$和$\frac{1}{4}$;
(3)由题意知:点M在OB和BE的垂直平分线上,
设OB和BE的垂直平分线交于点M,
其中OB的垂直平分线与OB交于点G,
BE的垂直平分线交OB于点H,交BE于点F
当点B在点D的右侧时,如图3,
∴6a>2,
∴a>$\frac{1}{3}$,
∴BD=6a-2,
∵tan∠EBD=$\frac{1}{2}$,
∴ED=$\frac{1}{2}$BD=3a-1,
由勾股定理可求得:BE=3$\sqrt{5}$a-$\sqrt{5}$,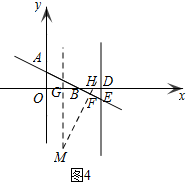
∴BF=$\frac{1}{2}$BE=$\frac{3\sqrt{5}a-\sqrt{5}}{2}$,
∴HF=$\frac{1}{2}$BF=$\frac{3\sqrt{5}a-\sqrt{5}}{4}$,
∴由勾股定理可求得:BH=$\frac{15a-5}{4}$,
∴HG=BG-BH=$\frac{5-3a}{4}$,
∵∠GMH=∠EBD,
∴sin∠GMH=sin∠EBD=$\frac{\sqrt{5}}{5}$,
∴MH=$\sqrt{5}$HG=$\frac{5\sqrt{5}-3\sqrt{5}a}{4}$,
∴MF=MH+HF=$\sqrt{5}$,
当点B在点D的左侧时,
∴0<a<$\frac{1}{3}$,
∴BD=OD-OB=2-6a,
∵tan∠ABO=tan∠DBE=$\frac{1}{2}$,
∴DE=$\frac{1}{2}$BD=1-3a,
∴由勾股定理可求得:BE=$\sqrt{5}$-3$\sqrt{5}$a,
∴BF=$\frac{1}{2}$BE=$\frac{\sqrt{5}-3\sqrt{5}a}{2}$,
∴HF=$\frac{1}{2}$BF=$\frac{\sqrt{5}-3\sqrt{5}a}{4}$,
由勾股定理求得:BH=$\frac{5-15a}{4}$,
∵GB=$\frac{1}{2}$OB=3a,
∴GH=GB+BH=$\frac{5-3a}{4}$,
∵∠HBF+∠BHF=90°,
∠GMH+∠BHF=90°,
∴∠HBF=∠GMH,
∴sin∠HBF=sin∠GMH=$\frac{\sqrt{5}}{5}$,
∴MH=$\sqrt{5}$GH=$\frac{5\sqrt{5}-3\sqrt{5}a}{4}$,
∴MF=MH-HF=$\sqrt{5}$,
当点B与点D重合时,
此时a=$\frac{1}{3}$,
此情况不符合题意,舍去
综上所述,点M到直线AB的距离不会变化,始终为$\sqrt{5}$.
点评 本题考查二次函数的综合问题,涉及已知解析式求坐标的问题,相似三角形的性质与判定,需要学生利用分类讨论的思想解答,并且能灵活运用所学知识.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 170 | B. | 400 | C. | 1万 | D. | 3万 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{0.3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{20}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,已知点A(0,1),B(0,-1).点P是平面内任意一点,直线PA,PB与直线x=4分别交于M,N两点.若以MN为直径的圆恰好经过点C(2,0),则称此时的点P为理想点.
如图,在平面直角坐标系xOy中,已知点A(0,1),B(0,-1).点P是平面内任意一点,直线PA,PB与直线x=4分别交于M,N两点.若以MN为直径的圆恰好经过点C(2,0),则称此时的点P为理想点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1<x2<x3 | B. | x1<x3<x2 | C. | x2<x1<x3 | D. | x2<x3<x1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com