Question

6．如图，在每个小正方形的边长为1的网格中，点A，B，C均在格点上．
（Ⅰ）△ABC的面积为12；
（Ⅱ）请在如图所示的网格中，用无刻度的直尺和圆规画出与△ABC的面积相等的正方形的一条边，并简要说明画法（不要求证明，保留作图痕迹）．画射线OK，再在OK上截取OM=3，作直角三角形OMN，是另一直角边NM=1，连接ON，．则NO长为$\sqrt{10}$，利用圆规以O为圆心，ON长为半径，在OK上截取OL=$\sqrt{10}$，再以OL为直角边，L为直角顶点再画直角三角形OLE，则OE=$\sqrt{11}$，再利用圆规以O为圆心，OE长为半径，在OK上截取OH=OE，再同法作直角三角形OHF，则OF=2$\sqrt{3}$，再利用圆规以O为圆心，OF长为半径，在OK上截取OG=OF，OF即为所求．

Answer 1

分析 （I）根据网格可得△ABC的底为6高为4，再利用三角形的面积公式进行计算即可．
（II）所画正方形的边长为2$\sqrt{3}$，利用勾股定理画图即可．

解答 解：（Ⅰ）△ABC的面积：6×4×$\frac{1}{2}$=12；

（II）如图所示：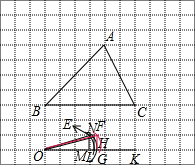
，
画射线OK，再在OK上截取OM=3，作直角三角形OMN，是另一直角边NM=1，连接ON，．
则NO长为$\sqrt{10}$，利用圆规以O为圆心，ON长为半径，在OK上截取OL=$\sqrt{10}$，再以OL为直角边，L为直角顶点再画直角三角形OLE，
则OE=$\sqrt{11}$，再利用圆规以O为圆心，OE长为半径，在OK上截取OH=OE，再同法作直角三角形OHF，则OF=2$\sqrt{3}$，
再利用圆规以O为圆心，OF长为半径，在OK上截取OG=OF，OF即为所求．
故答案为：画射线OK，再在OK上截取OM=3，作直角三角形OMN，是另一直角边NM=1，连接ON，．则NO长为$\sqrt{10}$，利用圆规以O为圆心，ON长为半径，在OK上截取OL=$\sqrt{10}$，再以OL为直角边，L为直角顶点再画直角三角形OLE，则OE=$\sqrt{11}$，再利用圆规以O为圆心，OE长为半径，在OK上截取OH=OE，再同法作直角三角形OHF，则OF=2$\sqrt{3}$，再利用圆规以O为圆心，OF长为半径，在OK上截取OG=OF，OF即为所求．

点评 此题主要考查了复杂作图，关键是掌握勾股定理：两直角边长的平方和等于斜边的平方．