
【题目】已知数3.3,-2,0,![]() ,-3.5.
,-3.5.
(1) 比较这些数的大小,并用“<”号连接起来;
(2) 比较这些数的绝对值的大小,并将这些数的绝对值用“>”号连接起来;
(3) 比较这些数的相反数的大小,并将这些数的相反数用“<”号连接起来.
【答案】(1)-3.5<-2<0<![]() <3.3;(2)3.5>3.3>2>
<3.3;(2)3.5>3.3>2>![]() >0;(3)-3.3<-
>0;(3)-3.3<-![]() <0<2<3.5
<0<2<3.5
【解析】
(1)利用有理数大小比较法则进行比较;
(2)先求得每个数的绝对值,再根据有理数大小比较法则进行比较大小;
(3) 先求得每个数的相反数,再根据有理数大小比较法则进行比较大小;
(1)正数都大于0;负数都小于0;正数大于一切负数;两个负数,绝对值大的其值反而小可得:-3.5<-2<0<![]() ;
;
(2)∵|-3.5|=3.5,|-2|=2,|0|=0,|![]() |=
|=![]()
∴3.5>3.3>2>![]() >0.
>0.
(3) 因为3.3的相反数是3.3,-2的相反数是2,0的相反数是0,![]() 和相反数是
和相反数是![]() ,-3.5的相反数是3.5,
,-3.5的相反数是3.5,
所以-3.3<-![]() <0<2<3.5.
<0<2<3.5.


科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 点A和点B位于直线l的两侧,如果A、B到l的距离相等,那么它们关于直线l对称
B. 两个全等的图形一定关于某条直线对称
C. 如果三角形中有一边的长度是另一边长度的一半,则这条边所对的角是30°
D. 等腰三角形一定是轴对称图形,对称轴有1条或者3条
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 6 |
第3组 | 35≤x<40 | 14 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解答过程:(1)如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
(2)如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
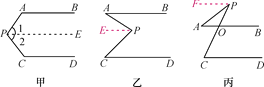
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线C:y=x2经过变化可得到抛物线C1:y1=a1x(x﹣b1),C1与x轴的正半轴交与点A1 , 且其对称轴分别交抛物线C,C1于点B1 , D1 , 此时四边形OB1A1D1恰为正方形;按上述类似方法,如图2,抛物线C1:y1=a1x(x﹣b1)经过变换可得到抛物线C2:y2=a2x(x﹣b2),C2与x轴的正半轴交与点A2 , 且其对称轴分别交抛物线C1 , C2于点B2 , D2 , 此时四边形OB2A2D2也恰为正方形;按上述类似方法,如图3,可得到抛物线C3:y3=a3x(x﹣b3)与正方形OB3A3D3 . 请探究以下问题: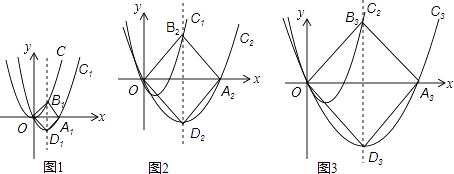
(1)填空:a1= , b1=;
(2)求出C2与C3的解析式;
(3)按上述类似方法,可得到抛物线Cn:yn=anx(x﹣bn)与正方形OBnAnDn(n≥1).
①请用含n的代数式直接表示出Cn的解析式;
②当x取任意不为0的实数时,试比较y2015与y2016的函数值的大小并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在直线AB上,点A1,A2,A3,…在射线OA上,点B1,B2,B3,…在射线OB上,图中的每一个实线段和虚线段的长均为1个单位长度.一个动点M从O点出发,按如图所示的箭头方向沿着实线段和以O为圆心的半圆匀速运动,速度为每秒1个单位长度.按此规律,则动点M到达A101点处所需时间为( )秒.
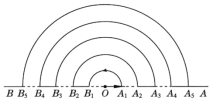
A. 5050π B. 5050π+101 C. 5055π D. 5055π+101
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下两小题后作出相应的解答:
(1)“同位角相等,两直线平行”,“两直线平行,同位角相等”,这两个命题的题设和结论在命题中的位置恰好对凋,我们把其中一命题叫做另一个命题的逆命题,请你写出命题“角平分线上的点到角两边的距离相等“的逆命题,并指出逆命题的题设和结论;
(2)根据以下语句作出图形,并写出该命题的文字叙述.
已知:过直线AB上一点O任作射线OC,OM、ON分别平分∠AOC、∠BOC,则OM⊥ON.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com