
【题目】京九铁路“南昌到赣州”段是连接省会城市与江西南大门城市的重要通道.一列快车从南昌开往赣州,列慢车从赣州开往南昌,两车同时出发,设慢车行驶的时间为![]() ,两车之间的距离为
,两车之间的距离为![]() ,图中的折线表示
,图中的折线表示![]() 与
与![]() 之间的函数关系.
之间的函数关系.
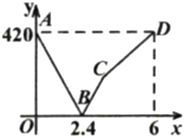
(1)慢车的速度为________![]() ,快车的速度为________
,快车的速度为________![]() ;
;
(2)当快车到达终点赣州后,求![]() 与
与![]() 之间的函数关系.
之间的函数关系.
【答案】(1)70,105;(2)![]()
【解析】
(1)设慢车的速度为m千米/时,快车的速度为n千米/时,有图像中的点B与点D的坐标的实际意义,列出二元一次方程组,即可求解;
(2)先求出当快车到达终点赣州时,所用的时间,以及两车的间距,从而得到点C的坐标,再用待定系数法,即可得到答案.
(1)设慢车的速度为m千米/时,快车的速度为n千米/时,由题意得:![]() ,
,
解得:![]() ,
,
答:慢车的速度为70![]() ,快车的速度为105
,快车的速度为105![]() .
.
故答案是:70,105;
(2)设当快车到达终点赣州后,![]() 与
与![]() 之间的函数关系式为:y=kx+b,
之间的函数关系式为:y=kx+b,
∵当快车到达终点赣州时,x=420÷105=4,y=(4-2.4)×(105+70)=280,
∴C(4,280),
∵D(6,420),
∴![]() ,解得:
,解得:![]() ,
,
∴当快车到达终点赣州后,![]() 与
与![]() 之间的函数关系为:
之间的函数关系为:![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,DE平分∠ADB,交AB于E,BF平分∠CBD,交CD于F.
(1)求证:△ADE≌△CBF;
(2)当AD与BD满足什么关系时,四边形DEBF是矩形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加快“智慧校园”建设,某市准备为试点学校采购一批![]() 、
、![]() 两种型号的一体机,经过市场调查发现,今年每套
两种型号的一体机,经过市场调查发现,今年每套![]() 型一体机的价格比每套
型一体机的价格比每套![]() 型一体机的价格多0.6万元,且用960万元恰好能购买500套
型一体机的价格多0.6万元,且用960万元恰好能购买500套![]() 型一体机和200套
型一体机和200套![]() 型一体机.
型一体机.
(1)求今年每套![]() 型、
型、![]() 型一体机的价格各是多少万元
型一体机的价格各是多少万元
(2)该市明年计划采购![]() 型、
型、![]() 型一体机1100套,考虑物价因素,预计明年每套
型一体机1100套,考虑物价因素,预计明年每套![]() 型一体机的价格比今年上涨25%,每套
型一体机的价格比今年上涨25%,每套![]() 型一体机的价格不变,若购买
型一体机的价格不变,若购买![]() 型一体机的总费用不低于购买
型一体机的总费用不低于购买![]() 型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生每周平均课外阅读时间(单位: ![]() ), 随机抽查了该学校九年级部分同学,对其每周平均课外阅读时间进行统计,绘制了如下的统计图①和②,请根据相关信息,解答下列问题;
), 随机抽查了该学校九年级部分同学,对其每周平均课外阅读时间进行统计,绘制了如下的统计图①和②,请根据相关信息,解答下列问题;
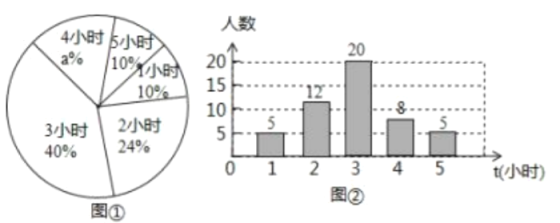
![]() 该校抽查九年级学生的人数为_______,图①中的 a值为______;
该校抽查九年级学生的人数为_______,图①中的 a值为______;
![]() 求统计的这组每周平均课外阅读时间的样本数据的平均数、众数和中位数;
求统计的这组每周平均课外阅读时间的样本数据的平均数、众数和中位数;
![]() 若该校九年级共有
若该校九年级共有![]() 名学生,根据统计的这组每周平均课外阅读时间的样本数据,估计该校九年级每周平均课外阅读时间为
名学生,根据统计的这组每周平均课外阅读时间的样本数据,估计该校九年级每周平均课外阅读时间为![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知A![]() ,B
,B![]() 是一次函数y=kx+b与反比例函数
是一次函数y=kx+b与反比例函数![]() 图象的两个交点.
图象的两个交点.

(1) 根据图象回答:当x满足 ,一次函数的值小于反比例函数的值;
(2) 将直线AB沿y轴方向,向下平移n个单位,与双曲线![]() 有唯一的公共点时,求n的值;
有唯一的公共点时,求n的值;
(3) 如图2,P点在![]() 的图象上,矩形OCPD的两边OD、OC在坐标轴上,且OC=2OD,M、N分别为OC、OD的中点,PN与DM交于点E,直接写出四边形EMON的面积为 .
的图象上,矩形OCPD的两边OD、OC在坐标轴上,且OC=2OD,M、N分别为OC、OD的中点,PN与DM交于点E,直接写出四边形EMON的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]()
![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() .
.
(1)该抛物线的对称轴为直线![]() ________;
________;
(2)已知该抛物线的开口向下,当![]() 时,
时,![]() 的最大值是4,求此范围内
的最大值是4,求此范围内![]() 的最小值.
的最小值.
(3)在(2)的条件下,直线![]() 过点
过点![]() ,且与该抛物线的另一个交点为点
,且与该抛物线的另一个交点为点![]() ,点
,点![]() 为抛物线对称轴上的动点,当
为抛物线对称轴上的动点,当![]() 为等腰三角形时直接写出点
为等腰三角形时直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年非洲猪瘟疫情暴发后,今年猪肉价格不断走高,引起了民众与政府的高度关注,据统计:今年7月20日猪肉价格比今年年初上涨了60%,某市民今年7月20日在某超市购买1千克猪肉花了80元钱.
(1)问:今年年初猪肉的价格为每千克多少元?
(2)某超市将进货价为每千克65元的猪肉,按7月20日价格出售,平均一天能销售出100千克,经调查表明:猪肉的售价每千克下降1元,其日销售量就增加10千克,超市为了实现销售猪内每天有1560元的利润,并且可能让顾客得到实惠,猪肉的售价应该下降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
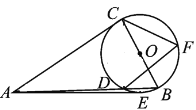
【题目】如图,Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E、F是⊙O上的两点,连结AE、CF、DF,满足EA=CA.
(1)求证:AE是⊙O的切线;
(2)若⊙O的半径是3,tan∠CFD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,∠C=90°,O是斜边AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与BC交于点F,与AC相切于点D,连接DF、BD,且BD平分∠ODF.
中,∠C=90°,O是斜边AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与BC交于点F,与AC相切于点D,连接DF、BD,且BD平分∠ODF.
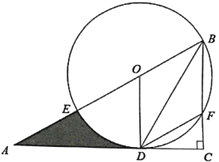
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,求阴影部分的面积(结果保留
,求阴影部分的面积(结果保留![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com