
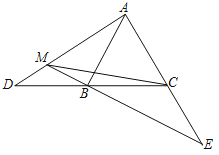
【题目】如图,在等边△ABC中,AB=4,D、E分别为射线CB、AC上的两动点,且BD=CE,直线AD和BE相交于M点,则CM的最大值为( )
A.2![]() B.
B.![]() C.3
C.3![]() D.4
D.4![]()
【答案】D
【解析】
首先证明∠AMB=60°,推出点M的运动轨迹是图中红线(在△ABM的外接圆⊙J上),连接CJ,延长CJ交⊙J 于N,当点M与N重合时,CM的值最大.
如图,
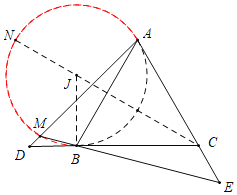
∵△ABC是等边三角形,
∴BA=CB,∠ABC=∠ACB=60°,
∴∠ABD=∠BCE=120°,
∵BD=CE,
∴△ABD≌△BCE(SAS),
∴∠D=∠E,
∵∠DBM=∠EBC,
∴∠DMB=∠BCE=120°,
∴∠AMB=60°,
∴点M的运动轨迹是图中红线(在△ABM的外接圆⊙J上),
连接CJ,延长CJ交⊙J 于N,当点M与N重合时,CM的值最大,
在Rt△JCB中,BJ=BCtan30=![]() ,JC=2BJ=
,JC=2BJ=![]() ,
,
∴CN=![]() +
+![]() =4
=4![]() ,
,
∴CM的最大值为4![]() ,
,
故选:D.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】有4张看上去无差别的卡片,上面分别写着1,2,3,4.
(1)一次性随机抽取2张卡片,求这两张卡片上的数字之和为奇数的概率;
(2)随机摸取1张后,放回并混在一起,再随机抽取1张,求两次取出的卡片上的数字之和等于4的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
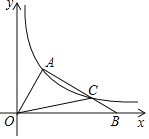
【题目】如图,在平面直角坐标系xOy中,△OAB的边OB在x轴上,过点A的反比例函数y=![]() 的图象交AB于点C,且AC:CB=2:1,S△OAC=
的图象交AB于点C,且AC:CB=2:1,S△OAC=![]() ,则k的值为( )
,则k的值为( )
A.![]() B.
B.![]() C.2D.2
C.2D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:点A与⊙O上所有点的连线段中,长度的最小值称为点A到⊙O的最小距离,记为mA;点A与⊙O上所有点的连线段中,长度的最大值称为点A到⊙O的最大距离,记为MA,如图,⊙O的半径为r,点A在⊙O外,且OA=d,则mA=d﹣r.证明如下:
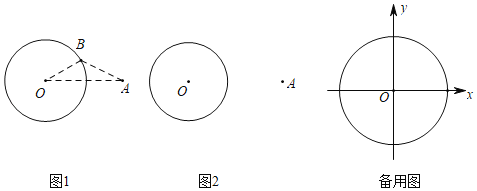
证明:如图1,设B为圆上任意一点,连结OA、OB、AB
①当O、A、B不共线时,AB>OA﹣OB
即AB>d﹣r
②当O、A、B共线时,AB=OA﹣OB
即AB=d﹣r
综上,AB≥d﹣r,即mA=d﹣r
(1)利用刚才的证明,结合所给的图2,⊙O的半径为r,点A在⊙O外,且OA=d,探究MA,你的结论是MA= ,请证明你的结论;
(2)已知⊙O的半径为2,mA=4,则MA= ;
(3)在平面直角坐标系中,以原点O为圆心,6为半径作⊙O,第二象限的点A的坐标为(﹣3,a),且mA=1,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
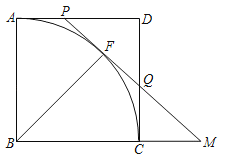
【题目】如图,在边长为5的正方形中,以B为圆心,BA为半径作弧AC,F为弧AC上一动点,过点F作⊙B的切线交AD于点P,交DC于点Q.
(1)求证:PQ=AP+CQ;
(2)分别延长PQ、BC,延长线相交于点M,如果AP=2,求BM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
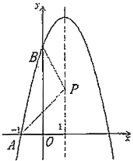
【题目】已知抛物线![]() 在坐标系中的位置如图所示,它与
在坐标系中的位置如图所示,它与![]() ,
,![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() ,
,![]() 是其对称轴
是其对称轴![]() 上的动点,根据图中提供的信息,给出以下结论:①
上的动点,根据图中提供的信息,给出以下结论:①![]() ,②
,②![]() 是
是![]() 的一个根,③若
的一个根,③若![]() ,
,![]() ,则
,则![]() .其中正确的有______个.
.其中正确的有______个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com