
��֪����x��һԪ���η���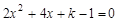 ��ʵ������kΪ������.
��ʵ������kΪ������.
������k��ֵ��
�����˷��������������������ʱ��������x�Ķ��κ���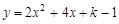 ��ͼ������ƽ��8����λ���ȣ���ƽ�ƺ��ͼ��Ľ���ʽ��
��ͼ������ƽ��8����λ���ȣ���ƽ�ƺ��ͼ��Ľ���ʽ��
�����ڣ��������£���ƽ�ƺ�Ķ��κ�����ͼ����x���·��IJ�����x�ᷭ�ۣ�ͼ������ಿ�ֱ��ֲ��䣬�õ�һ���µ�ͼ������������µ�ͼ��ش𣺵�ֱ��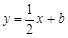 ��b��k�����ͼ��������������ʱ��b��ȡֵ��Χ��
��b��k�����ͼ��������������ʱ��b��ȡֵ��Χ��
���⣺������á�=16��8��k��1��=24��8k��0����k��3.
�֡�kΪ����������k=1��2��3.
����k=1ʱ������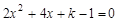 ��һ����Ϊ�㣻
��һ����Ϊ�㣻
��k=2ʱ������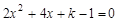 ����������
����������
��k=3ʱ������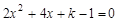 �����������������.
�����������������.
����������k=1��k=2�������⣬��ȥ. k=3��������.
��k=3ʱ�����κ���Ϊ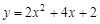 .
.
�Ѷ��κ���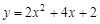 ��ͼ������ƽ��8����λ���ȵõ���
��ͼ������ƽ��8����λ���ȵõ���
ͼ�����ʽΪ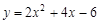 .
.
��������κ���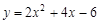 ��ͼ����x�ύ��A��B���㣬��A����3��0����B��1��0��.
��ͼ����x�ύ��A��B���㣬��A����3��0����B��1��0��.
�����ⷭ�ۺ��ͼ����ͼ.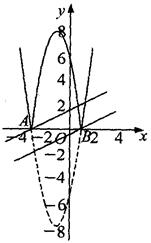
��ֱ��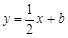 ������A����3��0��ʱ��b=
������A����3��0��ʱ��b= .
.
��ֱ��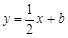 ������B��1��0��ʱ��b=
������B��1��0��ʱ��b=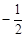 .
.
��ͼ���֪�����������b��b��3����ȡֵ��ΧΪ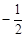 ��b��
��b��
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| x1 |
| 1 |
| x2 |
| A��8 | B��-7 | C��6 | D��5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����23�¡�һԪ���η��̡��п��⼯��23����23.3 ʵ����̽���������棩 ���ͣ������
 ��
���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2007��ȫ���п���ѧ�����ࡶһԪ���η��̡���04���������棩 ���ͣ������
 ��
���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com