
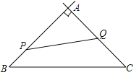
【题目】如图,△ABC中,∠ACB=90°,D为AB上任一点,过D作AB的垂线,分别交边AC、BC的延长线于EF两点,∠BAC∠BFD的平分线交于点I,AI交DF于点M,FI交AC于点N,连接BI.下列结论:
①∠BAC=∠BFD;
②∠ENI=∠EMI;
③AI⊥FI;
④∠ABI=∠FBI;
其中正确结论的个数是( )

A.1个 B.2个 C.3个 D.4个
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知,如图,![]() 垂直
垂直![]() ,AB=6,Δ
,AB=6,Δ![]() 是等边三角形,点
是等边三角形,点![]() 在射线
在射线![]() 上运动,以
上运动,以![]() 为边向右上方作等边Δ
为边向右上方作等边Δ![]() ,射线
,射线![]() 与射线
与射线![]() 交于点
交于点![]() .
.
(1)如图1,当点![]() 运动到与点
运动到与点![]() 成一条直线时,
成一条直线时,![]() (填长度),∠
(填长度),∠![]() 度.
度.

(2)在图2中,①求证:∠![]() ;
;
②随着点![]() 的运动,∠
的运动,∠![]() 的度数是否发生改变?若不变,求出这个角的度数;若改变,说明理由.
的度数是否发生改变?若不变,求出这个角的度数;若改变,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+2分别与x轴、y轴相交于点A、点B
x+2分别与x轴、y轴相交于点A、点B

(1)求点A和点B的坐标;
(2)若点P是y轴上的一点,设△AOB、△ABP的面积分别为S△AOB与S△ABP,且S△ABP=2S△AOB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,现有动点
,现有动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向运动,动点
方向运动,动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向运动,已知点
方向运动,已知点![]() 的速度是
的速度是![]() ,点
,点![]() 的速度是
的速度是![]() ,它们同时出发,经过________秒,
,它们同时出发,经过________秒,![]() 的面积是
的面积是![]() 面积的一半?
面积的一半?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县某商场计划购进甲、乙两种商品共80件,这两种商品的进价、售价如表所示:
进价(元/件) | 售价(元/件) | |
甲种商品 | 15 | 20 |
乙种商品 | 25 | 35 |
设其中甲种商品购进x件,售完此两种商品总利润为y元.
(1)写出y与x的函数关系式.
(2)该商场计划最多投入1500元用于购进这两种商品共80件,则至少要购进多少件甲种商品?若售完这些商品,商场可获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)(题文)等边![]() 在平面直角坐标系中,已知点
在平面直角坐标系中,已知点![]() ,将
,将![]() 绕点O顺时针方向旋转
绕点O顺时针方向旋转![]() 得
得![]() .
.
![]() 求出点B的坐标;
求出点B的坐标;
![]() 当
当![]() 与
与![]() 的纵坐标相同时,求出a的值;
的纵坐标相同时,求出a的值;
![]() 在
在![]() 的条件下直接写出点
的条件下直接写出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在关于x的分式方程![]() ①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.
①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.
(1)求k的取值范围;
(2)当方程②有两个整数根x1、x2,k为整数,且k=m+2,n=1时,求方程②的整数根;
(3)当方程②有两个实数根x1、x2,满足x1(x1﹣k)+x2(x2﹣k)=(x1﹣k)(x2﹣k),且k为负整数时,试判断|m|≤2是否成立?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com