
如图1,点A是线段BC上一点,△ABD和△ACE都是等边三角形.
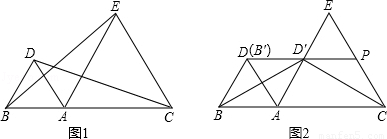
(1)连结BE,CD,求证:BE=CD;
(2)如图2,将△ABD绕点A顺时针旋转得到△AB′D′.
①当旋转角为 度时,边AD′落在AE上;
②在①的条件下,延长DD’交CE于点P,连接BD′,CD′.当线段AB、AC满足什么数量关系时,△BDD′与△CPD′全等?并给予证明.
解:(1)证明:∵△ABD和△ACE都是等边三角形, ∴AB=AD,AE=AC,∠BAD=∠CAE=60°。
∴∠BAD+∠DAE=∠CAE+∠DAE,即∠BAE=∠DAC。
在△BAE和△DAC中,∵AB=AD,∠BAE=∠DAC,AE=AC,
∴△BAE≌△DAC(SAS)。∴BE=CD。
(2)① 60。
②当AC=2AB时,△BDD′与△CPD′全等。理由如下:
由旋转可知,AB′与AD重合,∴AB=BD=DD′=AD′。
∴四边形ABDD′是菱形。
∴∠ABD′=∠DBD′=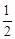 ∠ABD=
∠ABD=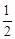 ×60°=30°,DP∥BC。
×60°=30°,DP∥BC。
∵△ACE是等边三角形,∴AC=AE,∠ACE=60°。
∵AC=2AB,∴AE=2AD′。
∴∠PCD′=∠ACD′=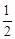 ∠ACE=
∠ACE=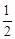 ×60°=30°。
×60°=30°。
又∵DP∥BC,∴∠ABD′=∠DBD′=∠BD′D=∠ACD′=∠PCD′=∠PD′C=30°。
在△BDD′与△CPD′中,∵∠DBD′=∠PCD′,BD′=CD′,∠BD′D=∠PD′C,
∴△BDD′≌△CPD′(ASA)。
【解析】
试题分析:(1)根据等边三角形的性质可得AB=AD,AE=AC,∠BAD=∠CAE=60°,然后求出∠BAE=∠DAC,再利用“边角边”证明△BAE和△DAC全等,根据全等三角形对应边相等即可得证;
(2)①求出∠DAE,即可得到旋转角度数:
∵∠BAD=∠CAE=60°,∴∠DAE=180°﹣60°×2=60°。
∵边AD′落在AE上,∴旋转角=∠DAE=60°。
②当AC=2AB时,△BDD′与△CPD′全等.根据旋转的性质可得AB=BD=DD′=AD′,然后得到四边形
ABDD′是菱形,根据菱形的对角线平分一组对角可得∠ABD′=∠DBD′=30°,菱形的对边平行可得DP∥BC,根据等边三角形的性质求出AC=AE,∠ACE=60°,然后根据等腰三角形三线合一的性质求出∠PCD′=∠ACD′=30°,从而得到∠ABD′=∠DBD′=∠BD′D=∠ACD′=∠PD′C=30°,然后利用“角边角”证明△BDD′与△CPD′全等。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com