
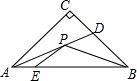
 如图所示,Rt△ABC中,AC=BC=4,AD平分∠BAC,点E在边AB上,且AE=1,点P是线段AD上的一个动点,则PE+PB的最小值等于5.
如图所示,Rt△ABC中,AC=BC=4,AD平分∠BAC,点E在边AB上,且AE=1,点P是线段AD上的一个动点,则PE+PB的最小值等于5.  暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
 阅读下面材料:在数学课上,老师提出如下问题:尺规作图:
阅读下面材料:在数学课上,老师提出如下问题:尺规作图:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A′O′B′=∠AOB的依据是( )
请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A′O′B′=∠AOB的依据是( )| A. | SAS | B. | SSS | C. | AAS | D. | ASA |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向左平移3个单位长度得到 | B. | 向右平移三个单位长度得到 | ||
| C. | 向上平移3个单位长度得到 | D. | 向下平移3个单位长度得到 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
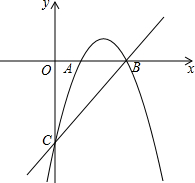 在平面直角坐标系xOy中,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),直线y=kx-3经过B、C两点.
在平面直角坐标系xOy中,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),直线y=kx-3经过B、C两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
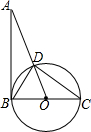 如图,AB=12,且AB为⊙O的切线,BC为⊙O的直径,AO与⊙O交于点D、AD=8.
如图,AB=12,且AB为⊙O的切线,BC为⊙O的直径,AO与⊙O交于点D、AD=8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 它是一个无理数 | |
| B. | 它是数轴上离原点$\sqrt{7}$个单位长度的点表示的数 | |
| C. | 若a<$\sqrt{7}$<a+1,则整数a为2 | |
| D. | 它表示面积为7的正方形的边长 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com