
【题目】如图,AC是![]() 的直径,BC切
的直径,BC切![]() 于点C,AB交
于点C,AB交![]() 于点D,BC的中点为E,连接DE.
于点D,BC的中点为E,连接DE.
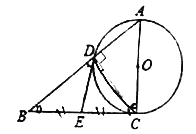
(1)求证:![]()
(2)连接E0交![]() 于点F填空:
于点F填空:
①当![]() __________时,以D,E,C,O为顶点的四边形是正方形;
__________时,以D,E,C,O为顶点的四边形是正方形;
②当![]() ______________时,以A,D,E,O为顶点的四边形是平行四边形
______________时,以A,D,E,O为顶点的四边形是平行四边形
【答案】(1)答案见解析;(2)①45°;②45°
【解析】
(1)根据直径所对的圆周角和直角三角形斜边中线的性质即可证明;(2)①如图,当∠B=45°时,以D,E,C,0为顶点的四边形是正方形;根据直径所对的圆周角是90°和全等三角形的判定先证△EOD≌△EOC,再结合(1)和∠B=45°,即可证四边形为正方形;②如图,利用①可证DE=OA,DE∥OA即可.
证明:(1)∵AC是直径
∴∠ADC=90°
∴∠BDC=90°
∴△BCD是直角三角形
又∵BE=CE
∴DE=CE=BE
∴BE=DE
(2)①连接OE,OD,如图,当∠B=45°时,以D,E,C,O为顶点的四边形是正方形
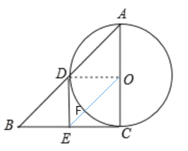
理由:∵BC是![]() 的切线
的切线
∴AC⊥BC,∠ACB=90°
∵OD=OC,OE=OE,DE=CE
∴△EOD≌△EOC(SSS)
∴∠EDO=∠ECO=90°
∵EB=ED
∴∠B=∠EDB=45°
∴∠DEC=∠B+∠EDB=90°
∴四边形DECO是矩形
∵OD=OC
∴矩形DECO是正方形
故答案为45°;
②如下图,结论∠B=45°

理由:当∠B=45°时,由①可知四边形DECO是正方形
∴DE∥OC,DE=OC
∵OA=OC
∴DE=OA
∴DE=OA,且DE∥OA
∴四边形ADEO是平行四边形
故答案为45°.


科目:初中数学 来源: 题型:
【题目】某区域平面示意图如图,点O在河的一侧,AC和BC表示两条互相垂直的公路.甲勘测员在A处测得点O位于北偏东45°,乙勘测员在B处测得点O位于南偏西73.7°,测得AC=840m,BC=500m.请求出点O到BC的距离.参考数据:sin73.7°≈![]() ,cos73.7°≈
,cos73.7°≈![]() ,tan73.7°≈
,tan73.7°≈![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD∥BC,AB⊥BC,AB=3.点E为射线 BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为__________ .
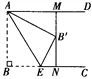
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋中有分别标有汉字“我”、“的”、“祖”、“国”的四个小球,除汉字外没有任何区别,每次摸球前先摇匀再摸球.
(1)若从中任意摸一个球,求摸出球上的汉字刚好是“国”字的概率;
(2)小林从中任取一个球,记下汉字后放回,摇匀后再从中任取一个.请用树状图或列表法,求小林取出的两个球上的汉字恰好能组成“祖国”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题.
例:用图象法解一元二次不等式:![]()
解:设![]() ,则
,则![]() 是
是![]() 的二次函数.∵
的二次函数.∵![]() ,
,
∴抛物线开口向上.
又∵当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() .
.
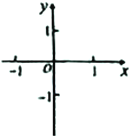
∴由此得抛物线![]() 的大致图象如图所示.
的大致图象如图所示.

观察函数图象可知:当![]() 或
或![]() 时,
时,![]() .
.
∴![]() 的解集是:
的解集是:![]() 或
或![]() .
.
(1)观察图象,直接写出一元二次不等式:![]() 的解集是______;
的解集是______;
(2)仿照材料、用图象法解一元二次不等式:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x﹣3)2+![]() 过点C(0,4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:①抛物线的对称轴是直线x=3;②点C在⊙D外;③在抛物线上存在一点E,能使四边形ADEC为平行四边形;④直线CM与⊙D相切.正确的结论是( )
过点C(0,4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:①抛物线的对称轴是直线x=3;②点C在⊙D外;③在抛物线上存在一点E,能使四边形ADEC为平行四边形;④直线CM与⊙D相切.正确的结论是( )
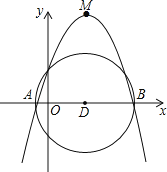
A.①③B.①④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中xOy中,抛物线y=ax2﹣4ax+1.
(1)求抛物线的对称轴;
(2)若抛物线过点A(﹣1,6),求二次函数的表达式;
(3)若抛物线与坐标轴只有两个交点,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标平面内,小明站在点A(﹣10,0)处观察y轴,眼睛距地面1.5米,他的前方5米处有一堵墙DC,若墙高DC=2米,则小明在y轴上的盲区(即OE的长度)为_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
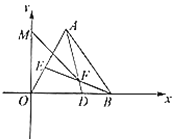
【题目】如图,在平面直角坐标系中,等边![]() 的边
的边![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() ,
,![]() ,点
,点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 出发以相同的速度向
出发以相同的速度向![]() 、
、![]() 运动,连接
运动,连接![]() 、
、![]() 交于点
交于点![]() ,
,![]() 是
是![]() 轴上一点,则
轴上一点,则![]() 的最小值为______.
的最小值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com