
已知二次函数y=a(x-m)2-a(x-m)(a,m为常数,且a≠0).
(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点;
(2)设该函数的图象的顶点为C,与x轴交于A,B两点,与y轴交于点D.
①当△ABC的面积等于1时,求a的值;
②当△ABC的面积与△ABD的面积相等时,求m的值.
(1)证明:y=a(x-m)2-a(x-m)=ax2-(2am+a)x+am2+am.
当a≠0时,Δ=a2>0.
则方程ax2-(2am+a)x+am2+am=0有两个不相等的实数根.
所以,不论a与m为何值,该函数的图象与x轴总有两个公共点.
(2)解:① y=a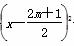 -
-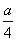 ,
,
所以点C的坐标为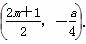 .
.
当y=0时,a(x-m)2-a(x-m)=0.
解得x1=m,x2=m+1.所以AB=1.
当△ABC的面积等于1时,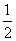 ×1×
×1×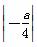 =1.
=1.
所以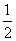 ×1×
×1×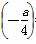 =1,或
=1,或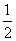 ×1×
×1×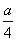 =1.
=1.
所以a=-8,或a=8.
②当x=0时,y=am2+am,
所以点D的坐标为(0, am2+am).
当△ABC的面积与△ABD的面积相等时,
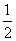 ×1×
×1×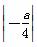 =
=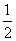 ×1×| am2+am |.
×1×| am2+am |.
所以m=-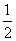 ,或m=
,或m=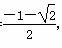 ,或m=
,或m=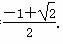 .
.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
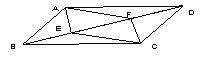
如图,在四边形ABCD中AB//CD,若加上AD//BC,则四边形ABCD为平行四边形。现在请你添加一个适当的条件: ,使得四边形AECF为平行四边形.( 图中不再添加点和线)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图N21,C,B是线段AD上的两点,若AB=CD,BC=2AC,那么AC与CD的关系是为( )

图N21
A.CD=2AC B.CD=3AC
C.CD=4BD D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
在6张完全相同的卡片上分别画上线段、等边三角形、平行四边形、直角梯形、正方形和圆.在看不见图形的情况下随机摸出1张,是中心对称图形的概率是( )
A.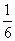 B.
B.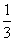 C.
C.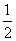 D.
D.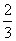
查看答案和解析>>
科目:初中数学 来源: 题型:
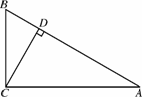
如图N44,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D.则△BCD与△ABC的周长之比为( )
A.1∶5 B.1∶4 C.1∶3 D.1∶2
查看答案和解析>>
科目:初中数学 来源: 题型:
根据下列表格中的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的个数是( )
A.0 B.1 C.2 D.1或2
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y=ax2+bx+c | 0.02 | -0.01 | 0.02 | 0.04 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com