
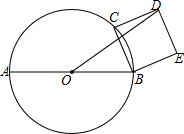
 如图,AB为⊙O的直径,AB=4,点C为半圆AB上动点,以BC为边在⊙O外作正方形BCDE,(点D在直线AB的上方)连接OD.当点C运动时,则线段OD的长( )
如图,AB为⊙O的直径,AB=4,点C为半圆AB上动点,以BC为边在⊙O外作正方形BCDE,(点D在直线AB的上方)连接OD.当点C运动时,则线段OD的长( )| A. | 随点C的运动而变化,最大值为2+2$\sqrt{2}$ | B. | 不变 | ||
| C. | 随点C的运动而变化,最大值为2$\sqrt{2}$ | D. | 随点C的运动而变化,但无最值 |
分析 通过旋转观察如图可知当DO⊥AB时,DO最长,设DO与⊙O交于点M,连接CM,先证明△MED≌△MEB,得MD=BM.再利用勾股定理计算即可.
解答 解:通过旋转观察如图可知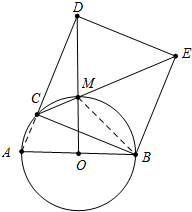 当DO⊥AB时,DO最长,设DO与⊙O交于点M,连接CM,
当DO⊥AB时,DO最长,设DO与⊙O交于点M,连接CM,
∵∠MCB=$\frac{1}{2}$MOB=$\frac{1}{2}$×90°=45°,
∴∠DCM=∠BCM=45°,
∵四边形BCDE是正方形,
∴C、M、E共线,∠DEM=∠BEM,
在△EMD和△EMB中,
$\left\{\begin{array}{l}{DE=BC}\\{∠MED=∠MEB}\\{ME=ME}\end{array}\right.$,
∴△MED≌△MEB,
∴DM=BM=$\sqrt{O{M}^{2}+O{B}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∴OD的最大值=2+2$\sqrt{2}$.
故选A.
点评 本题考查正方形的性质、圆周角定理等知识,解题的关键是OD取得最大值时的位置,学会通过特殊位置探究得出结论,属于中考常考题型.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:初中数学 来源: 题型:解答题
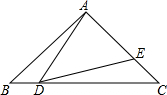 如图.在△ABC中.AB=AC=9,BC=12,∠B=∠C,点D从B出发以每秒2厘米的速度在线BC上从B向C方向运动,点E同时从C出发以每秒2厘米的速度在线段AC上从C向A运动,连接AD、DE;
如图.在△ABC中.AB=AC=9,BC=12,∠B=∠C,点D从B出发以每秒2厘米的速度在线BC上从B向C方向运动,点E同时从C出发以每秒2厘米的速度在线段AC上从C向A运动,连接AD、DE;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
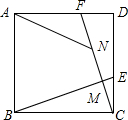 如图,E,F分别是边长为6的正方形ABCD的边CD,AD上两点,且CE=DF,连接CF,BE交于点M,在MF上截取MN=MC,连接AN,若FN=$\frac{4}{3}$CM,则AN的长度为$\frac{12\sqrt{5}}{5}$.
如图,E,F分别是边长为6的正方形ABCD的边CD,AD上两点,且CE=DF,连接CF,BE交于点M,在MF上截取MN=MC,连接AN,若FN=$\frac{4}{3}$CM,则AN的长度为$\frac{12\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
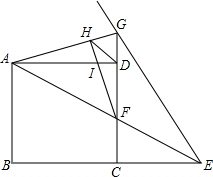 如图,已知正方形ABCD,E为BC延长线上一点,连AE交CD于F,作∠AEG=∠AEB,EG交CD于G连AG,作FH⊥AG于H,连DH.下列说法正确的是( )
如图,已知正方形ABCD,E为BC延长线上一点,连AE交CD于F,作∠AEG=∠AEB,EG交CD于G连AG,作FH⊥AG于H,连DH.下列说法正确的是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
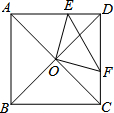 如图,在正方形ABCD中,O是对角线的交点,过点O作OE⊥OF,分别交AD,CD于E,F,若AE=6,CF=4,则EF=2$\sqrt{13}$.
如图,在正方形ABCD中,O是对角线的交点,过点O作OE⊥OF,分别交AD,CD于E,F,若AE=6,CF=4,则EF=2$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
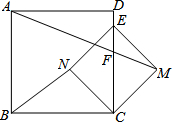 如图,在正方形ABCD中,E为CD边上一点,以CE为对角线构造正方形CMEN,点N在正方形ABCD内部,连接AM,与CD边交于点F.若CF=3,DF=2,连接BN,则BN的长为$\frac{25}{7}$.
如图,在正方形ABCD中,E为CD边上一点,以CE为对角线构造正方形CMEN,点N在正方形ABCD内部,连接AM,与CD边交于点F.若CF=3,DF=2,连接BN,则BN的长为$\frac{25}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
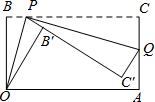 已知一个矩形纸片OACB,OB=6,OA=11,点P为BC边上的动点(点P不与点B,C重合),经过点O折叠该纸片,得折痕OP和点B′,经过点P再次折叠纸片,使点C落在直线PB′上,得折痕PQ和点C′,当点C′恰好落在边OA上时BP的长为
已知一个矩形纸片OACB,OB=6,OA=11,点P为BC边上的动点(点P不与点B,C重合),经过点O折叠该纸片,得折痕OP和点B′,经过点P再次折叠纸片,使点C落在直线PB′上,得折痕PQ和点C′,当点C′恰好落在边OA上时BP的长为查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com