
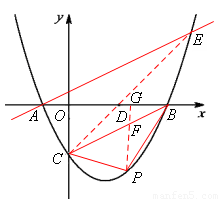
如图,已知抛物线 (b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).

(1)b= ,点B的横坐标为 (上述结果均用含c的代数式表示);
(2)连接BC,过点A作直线AE∥BC,与抛物线 交于点E.点D是x轴上一点,其坐标为
交于点E.点D是x轴上一点,其坐标为
(2,0),当C,D,E三点在同一直线上时,求抛物线的解析式;
(3)在(2)的条件下,点P是x轴下方的抛物线上的一动点,连接PB,PC,设所得△PBC的面积为S.
①求S的取值范围;
②若△PBC的面积S为整数,则这样的△PBC共有 个.
解:(1)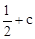 ;
;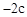 。
。
(2)在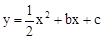 中,令x=0,得y=c,
中,令x=0,得y=c,
∴点C的坐标为(c,0)。
设直线BC的解析式为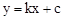 ,
,
∵点B的坐标为(-2 c,0),∴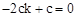 。
。
∵ ,∴
,∴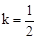 。
。
∴直线BC的解析式为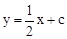 。
。
∵AE∥BC,∴可设直线AE的解析式为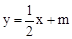 。
。
∵点A的坐标为(-1,0),∴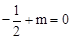 ,
,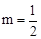 。
。
∴直线AE的解析式为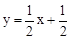 。
。
由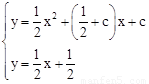 解得
解得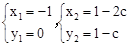 。
。
∴点E的坐标为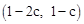 。
。
∵点C的坐标为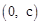 ,点D的坐标为(2,0),∴直线CD的解析式为
,点D的坐标为(2,0),∴直线CD的解析式为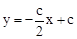 。
。
∵点C,D,E三点在同一直线上,∴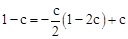 。
。
∴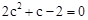 ,解得
,解得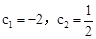 (舍去)。
(舍去)。
∴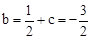 。
。
∴抛物线的解析式为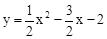 。
。
(3)①设点P的坐标为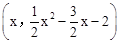 ,
,
∵点A的坐标为(-1,0),点B的坐标为(4,0),点C的坐标为(0,-2),
∴AB=5,OC=2,直线CB的解析式为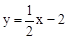 。
。
当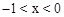 时,
时,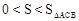 ,
,
∵ ,∴
,∴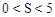 。
。
当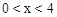 时,过点P作PG⊥x轴于点G,交BC于点F,
时,过点P作PG⊥x轴于点G,交BC于点F,
∴点F的坐标为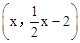 。
。
∴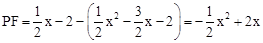 。
。
∴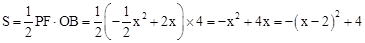 。
。
∴当x=2时, 。∴
。∴
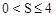 。
。
综上所述,S的取值范围为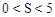 。
。
②11。
【解析】
试题分析:(1)将点A的坐标为(-1,0)代入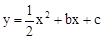 得
得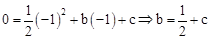 。
。
∴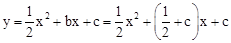 。
。
令 ,解得
,解得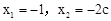 。
。
∴点B的横坐标为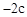 。
。
(2)求出直线BC的解析式,从而求出直线AE的解析式,得到点E的坐标为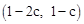 ,由点C,D,E三点在同一直线上,将
,由点C,D,E三点在同一直线上,将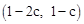 代入直线CD的解析式
代入直线CD的解析式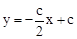 即可求出c,由(1)
即可求出c,由(1)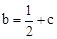 求出b,从而得到抛物线的解析式。
求出b,从而得到抛物线的解析式。
(3)①分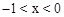 和
和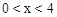 两种情况讨论。
两种情况讨论。
②当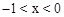 时,
时,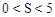 ,且S为整数,对应的x有4个;
,且S为整数,对应的x有4个;
当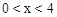 时,
时,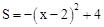 ,
,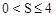 ,且S为整数,对应的x有7个(
,且S为整数,对应的x有7个(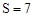 时只有1个)。
时只有1个)。
∴若△PBC的面积S为整数,则这样的△PBC共有11个。


 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
 C(0,3).
C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:
 、C(0,-3)两点,与x轴交于另一点B.
、C(0,-3)两点,与x轴交于另一点B.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;
如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com