
【题目】阅读下列材料并解决问题
进位制是一种记数方式,可以用有限的数字符号代表所有的数值,使用数字符号的数目称为基数,基数为n,即可称n进制。现在最常用的是十进制,通常使用10个阿拉伯数字0~9进行记数,特点是逢十进一。
对于任意一个用![]() 进制表示的数,通常使用n个阿拉伯数字
进制表示的数,通常使用n个阿拉伯数字![]() 进行记数,特点是逢n进一。我们可以通过以下方式把它转化为十进制:
进行记数,特点是逢n进一。我们可以通过以下方式把它转化为十进制:
例如:五进制数![]() ,记作:
,记作: ![]() ,
,
七进制数![]() ,记作:
,记作: ![]()
(1)请将以下两个数转化为十进制: ![]() ____________,
____________, ![]() ____________ ;
____________ ;
(2)若一个正数可以用七进制表示为![]() ,也可以用五进制表示为
,也可以用五进制表示为![]() ,请求出这个数并用十进制表示。
,请求出这个数并用十进制表示。
【答案】(1)82,83;(2)满足关系的整数a、b、c共有四种情形:(1) a=1,b=0,c=2,此数用十进制表示为:102;(2) a=2,b=0,c=4,此数用十进制表示为:204;(3) a=3,b=0,c=6,此数用十进制表示为:306;(4) a=4,b=0,c=8,此数用十进制表示为:408.
【解析】试题分析:(1)根据进制的计算规则列式计算即可得;
(2)由题意得出72a+7b+c=52c+5b+a,即24a+b=12c,结合1≤a≤9,0≤b≤9,1≤c≤9,且a、b、c均为整数得出a、b、c的值,表示成十进制即可.
(1) ![]() ___82___,
___82___, ![]() ___83____.
___83____.
(2)∵![]()
![]()
根据题意,得: ![]()
整理得: 24a+b=12c
∵ 1≤a≤9;0≤b≤9;0≤c≤9;且a、b、c均为整数
∴ 满足关系的整数a、b、c共有四种情形
(1) a=1,b=0,c=2,此数用十进制表示为:102
(2) a=2,b=0,c=4,此数用十进制表示为:204
(3) a=3,b=0,c=6,此数用十进制表示为:306
(4) a=4,b=0,c=8,此数用十进制表示为:408


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠BAC=90°,AB=6,AC=8,D 为 AC 上一点,将△ABD 沿 BD 折叠,使点 A 恰好落在 BC 上的 E 处,则折痕 BD 的长是( )

A.5B.![]() C.3
C.3 ![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )
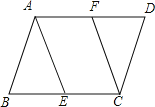
A. AF=CE B. AE=CF C. ∠BAE=∠FCD D. ∠BEA=∠FCE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东营市某中学校团委开展“关爱残疾儿童”爱心捐书活动,全校师生踊跃捐赠各类书籍共3000本.为了了解各类书籍的分布情况,从中随机抽取了部分书籍分四类进行统计:A.艺术类;B.文学类;C.科普类;D.其他,并将统计结果绘制成如图所示的两幅不完整的统计图.

(1)这次统计共抽取_____本书籍,扇形统计图中的m=______,∠α的度数是_____
(2)请将条形统计图补充完整;
(3)估计全校师生共捐赠了多少本文学类书籍.
查看答案和解析>>
科目:初中数学 来源: 题型:
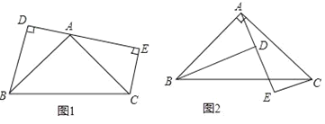
【题目】已知:如图1,AB=AC,点A是线段DE上一点,∠BAC=90°,BD⊥DE,CE⊥DE,
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,你能得到什么结论?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠A的平分线交BC于D. 过C点作CG⊥AB于G,交AD于E. 过D点作DF⊥AB于F. 下列结论:①∠CED=∠CDE;②S△AEC:S△AEG=AC:AG;③∠ADF=2∠FDB;④CE=DF.其中正确的结论有( )
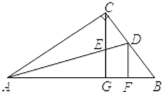
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,二次函数y=ax2+bx+c与x轴的交点为(x1,0),(x2,0),且x1<x2,若方程ax2+bx+c﹣a=0的两根为m,n(m<n),则下列说法正确的是( )
A. x1+x2>m+n B. m<n<x1<x2 C. x1<m<n<x2 D. m<x1<x2<n
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最大值是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com