
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0,x>0)的图象在第一象限内交于点A,B,且该一次函数的图象与y轴正半轴交于点C,过A,B分别作y轴的垂线,垂足分别为D,E.已知A(1,4),
(m≠0,x>0)的图象在第一象限内交于点A,B,且该一次函数的图象与y轴正半轴交于点C,过A,B分别作y轴的垂线,垂足分别为D,E.已知A(1,4),![]() =
=![]() .
.
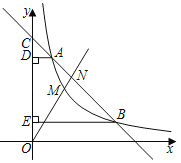
(1)求m的值和一次函数的解析式;
(2)若点M为反比例函数图象在A,B之间的动点,作射线OM交直线AB于点N,当MN长度最大时,直接写出点M的坐标.
【答案】(1)4,y=﹣x+5;(2)(2,2)
【解析】
(1)先把A点坐标代入y=![]() 中求出m得到反比例函数解析式为y=
中求出m得到反比例函数解析式为y=![]() ;再证明△CDA∽△CEB,利用相似比求出BE=4,则利用反比例函数解析式确定B点坐标,然后利用待定系数法求一次函数解析式;
;再证明△CDA∽△CEB,利用相似比求出BE=4,则利用反比例函数解析式确定B点坐标,然后利用待定系数法求一次函数解析式;
(2)利用点A与点B关于直线y=x对称,反比例函数y=﹣![]() 关于y=x对称可判断当OM的解析式为y=x时,MN的长度最大,然后解方程组
关于y=x对称可判断当OM的解析式为y=x时,MN的长度最大,然后解方程组![]() 得此时M点的坐标.
得此时M点的坐标.
(1)把A(1,4)代入y=![]() 得m=1×4=4,
得m=1×4=4,
∴反比例函数解析式为y=![]() ;
;
∵BD⊥y轴,AD⊥y轴,
∴AD∥BE,
∴△CDA∽△CEB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴BE=4,
当x=4时,y=![]() =
=![]() =1,
=1,
∴B(4,1),
把A(1,4),B(4,1)代入y=kx+b得![]() ,解得
,解得![]() ,
,
∴一次函数解析式为y=﹣x+5;
(2)∵点A与点B关于直线y=x对称,反比例函数y=﹣![]() 关于y=x对称,
关于y=x对称,
∴当OM的解析式为y=x时,MN的长度最大,
解方程组![]() 得
得![]() 或
或![]() ,
,
∴此时M点的坐标为(2,2).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
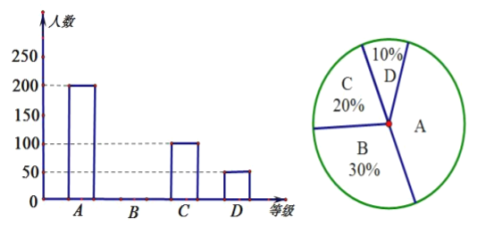
【题目】某学校为了调查同学们对学生会的满意度,随机抽取了部分同学作问卷调查:用“![]() ”表示“相 当满意”,“
”表示“相 当满意”,“![]() ”表示“满意”,“
”表示“满意”,“![]() ”表示“比较满意”,“
”表示“比较满意”,“![]() ”表示“不满意”,下图是负责 调查同学根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
”表示“不满意”,下图是负责 调查同学根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
(1)本次问卷调查,共调查了多少人;
(2)通过计算补全条形图;
(3)如果该学校有![]() 名学生,请你估计该校学生对学生会感到“相当满意”的约有多少人?
名学生,请你估计该校学生对学生会感到“相当满意”的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于两点
的图像交于两点![]() ,
,![]() .
.
(1)求反比例函数与一次函数的函数表达式;
(2)在反比例函数的图像上找点![]() ,使得点
,使得点![]() 构成以
构成以![]() 为底的等腰三角形,请求出所有满足条件的点
为底的等腰三角形,请求出所有满足条件的点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全球已经进入大数据时代,大数据(bigdata)是指数据规模巨大,类型多样且信息传播速度快的数据库体系.大数据在推动经济发展,改善公共服务等方面日益显示出巨大的价值.为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是根据调查结果绘制出不完整的两个统计图表:
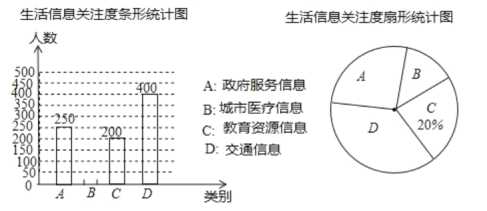
请根据图中提供的信息,解答下列问题:
(1)本次参与调查的人数是________,扇形统计图中![]() 部分的圆心角的度数是________,并补全条形统计图;
部分的圆心角的度数是________,并补全条形统计图;
(2)这次调查的市民最关心的四类生活信息的众数是________类;
(3)若我市现有常住人口约600万,请你估计最关心“城市医疗信息”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】党的十八大以来,全国各地认真贯彻精准扶贫方略,扶贫工作力度、深度和精准度都达到了新的水平,为2020年全面建成小康社会的战略目标打下了坚实基础.以下是根据近几年中国农村贫困人口数量(单位:万人)及分布情况绘制的统计图表的一部分.
年份 人数 地区 | 2017 | 2018 | 2019 |
东部 | 300 | 147 | 47 |
中部 | 1112 | 181 | |
西部 | 1634 | 916 | 323 |
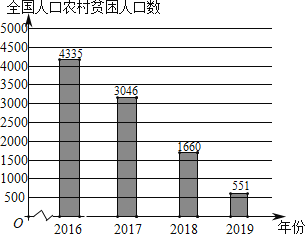
(以上数据来源于国家统计局)
根据统计图表提供的信息,下面推断不正确的是( )
A.2018年中部地区农村贫困人口为597万人
B.2017﹣2019年,农村贫困人口数量都是东部最少
C.2016﹣2019年,农村贫困人口减少数量逐年增多
D.2017﹣2019年,虽然西部农村贫困人口减少数量最多,但是相对于东、中部地区,它的降低率最低
查看答案和解析>>
科目:初中数学 来源: 题型:
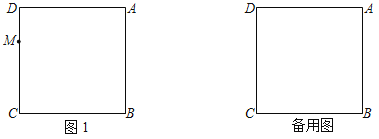
【题目】如图,在正方形ABCD中,AB=3,M是CD边上一动点(不与D点重合),点D与点E关于AM所在的直线对称,连接AE,ME,延长CB到点F,使得BF=DM,连接EF,AF.
(1)依题意补全图1;
(2)若DM=1,求线段EF的长;
(3)当点M在CD边上运动时,能使△AEF为等腰三角形,直接写出此时tan∠DAM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
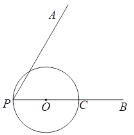
【题目】如图,∠APB,点C在射线PB上,PC为⊙O的直径,在∠APB内部且到∠APB两边距离都相等的所有的点组成图形M,图形M交⊙O于D,过点D作直线DE⊥PA,分别交射线PA,PB于E,F.
(1)根据题意补全图形;
(2)求证:DE是⊙O的切线;
(3)如果PC=2CF,且![]() ,求PE的长.
,求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的任意一点
中的任意一点![]() ,给出如下定义:经过点
,给出如下定义:经过点![]() 且平行于两坐标轴夹角平分线的直线,叫做点
且平行于两坐标轴夹角平分线的直线,叫做点![]() 的“特征线”.例如:点
的“特征线”.例如:点![]() 的特征线是
的特征线是![]() 和
和![]() .
.
(1)若点![]() 的其中一条特征线是
的其中一条特征线是![]() ,则在
,则在![]() 、
、![]() 、
、![]() 三个点中,可能是点
三个点中,可能是点![]() 的点有_______;
的点有_______;
(2)已知点![]() 的平行于第二、四象限夹角平分线的特征线与
的平行于第二、四象限夹角平分线的特征线与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,且与
,且与![]() 轴交于点
轴交于点![]() .使
.使![]() 的面积不小于6,求
的面积不小于6,求![]() 的取值范围;
的取值范围;
(3)已知点![]() ,
,![]() ,且
,且![]() 的半径为1.当
的半径为1.当![]() 与点
与点![]() 的特征线存在交点时,直接写出
的特征线存在交点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
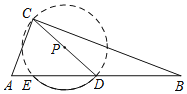
【题目】在△ABC中,以AB边上的中线CD为直径作圆,如果与边AB有交点E(不与点D重合),那么称![]() 为△ABC的C﹣中线弧.例如,如图中
为△ABC的C﹣中线弧.例如,如图中![]() 是△ABC的C﹣中线弧.在平面直角坐标系xOy中,已知△ABC存在C﹣中线弧,其中点A与坐标原点O重合,点B的坐标为(2t,0)(t>0).
是△ABC的C﹣中线弧.在平面直角坐标系xOy中,已知△ABC存在C﹣中线弧,其中点A与坐标原点O重合,点B的坐标为(2t,0)(t>0).
(1)当t=2时,
①在点C1(﹣3,2),C2(0,2![]() ),C3(2,4),C4(4,2)中,满足条件的点C是 ;
),C3(2,4),C4(4,2)中,满足条件的点C是 ;
②若在直线y=kx(k>0)上存在点P是△ABC的C﹣中线弧![]() 所在圆的圆心,其中CD=4,求k的取值范围;
所在圆的圆心,其中CD=4,求k的取值范围;
(2)若△ABC的C﹣中线弧![]() 所在圆的圆心为定点P(2,2),直接写出t的取值范围.
所在圆的圆心为定点P(2,2),直接写出t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com