练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
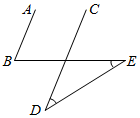
    7．如图，AB∥CD，∠D=∠E=35，则∠B的度数为（　　）
    A．60°B．65°C．70°D．75°

    分析 根据三角形的一个外角等于与它不相邻的两个内角的和，求出∠1，再根据两直线平行，同位角相等进行解答即可．

    解答 解：如图，∵∠D=∠E=35°，
    ∴∠1=∠D+∠E=35°+35°=70°，
    ∵AB∥CD，
    ∴∠B=∠1=70°．
    故选：C．

    点评 本题考查了平行线的性质，三角形的外角性质，熟记各性质并准确识图是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

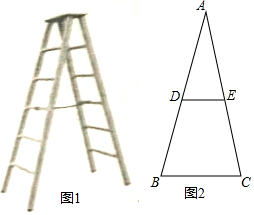    17．如图1所示的是由梯子AB和梯子AC搭成的“人字梯”，它的5个踩档把梯子等分成6份，梯子的第三踩档处有一条绑绳DE，将其抽象成图2，其中AB=AC=2米．
    （1）若DE的长为60厘米，求两梯角之间的距离BC的长．
    （2）若∠ABC=70°，小明想在人字梯的D，E处系上一根绳子确保用梯安全，在D，E处打结各需要0.3米的绳子，请你帮小明计算一下，他需要的绑绳的长度为多少米？此时梯子的顶端A离地面BC的高度为多少米？（结果精确到0.01厘米；参考数据：sin70°=0.9397，cos70°=0.3420，tan70°=2.7475）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图①，∠QPN的顶点P在正方形ABCD两条对角线的交点处，∠QPN=α，∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F（点F与点C、D不重合）．

    （1）如图①，当α=90°时，求证：DE+DF=AD．
    （2）如图②，将图①中的正方形ABCD改为∠ADC=120°的菱形，其他条件不变，当α=60°时，（1）中的结论变为$DE+DF=\frac{1}{2}AD$，请给出证明．
    （3）在（2）的条件下，将∠QPN绕点P旋转，若旋转过程中∠QPN的边PQ与边AD的延长线交于点E，其他条件不变，探究在整个运动变化过程中，DE，DF，AD之间满足的数量关系，直接写出结论，不用加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列各式中，正确的是（　　）
    A．m2•m3=m6B．（2a+b）（a-b）=2a2+ab-b2
    C．（5a+2b）（5a-3b）=25a2-6b2D．（x-y）（x2+xy+y2）=x3-y3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．甲乙两地相距72千米，李磊骑自行车往返两地一共用了7小时，已知他去时的平均速度比返回时的平均速度快$\frac{1}{3}$，求李磊去时的平均速度是多少？
    小芸同学解法如下：
    解：设李磊去时的平均速度是x千米/时，则返回时的平均速度是（1-$\frac{1}{3}$）x千米/时，由题意得：$\frac{72}{x}$+$\frac{72}{（1-\frac{1}{3}）x}$=7，…
    你认为小芸同学的解法正确吗？若正确，请写出该方程所依据的等量关系，并完成剩下的步骤；若不正确，请说明原因，并完整地求解问题．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如图所示，在每个边长都为1的小正方形组成的网格中，点A、B、C均为格点．
    （Ⅰ）线段AB的长度等于5；
    （Ⅱ）若P为线段AB上的动点，以PC、PA为邻边的四边形PAQC为平行四边形，当PQ长度最小时，请你借助网格和无刻度的直尺画出该平行四边形，并简要说明你的作图方法（不要求证明）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列计算中，正确的是（　　）
    A．a•a=2aB．x+x4=x5C．x3•x2=x5D．2a2•a-1=2a3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．对于一个三位正整数t，将各数位上的数字重新排序后（包括本身），得到一个新的三位数$\overline{abc}$（a≤c），在所有重新排列的三位数中，当|a+c-2b|最小时，称此时的$\overline{abc}$为t的“最优组合”，并规定F（t）=|a-b|-|b-c|，例如：124重新排序后为：142、214、因为|1+4-4|=1，|1+2-8|=5，|2+4-2|=4，所以124为124的“最优组合”，此时F（124）=-1．
    （1）三位正整数t中，有一个数位上的数字是另外两数位上的数字的平均数，求证：F（t）=0
    （2）一个正整数，由N个数字组成，若从左向右它的第一位数能被1整除，它的前两位数能被2整除，前三位数能被3整除，…，一直到前N位数能被N整除，我们称这样的数为“善雅数”．例如：123的第一位数1能披1整除，它的前两位数12能被2整除，前三位数123能被3整除，则123是一个“善雅数”．若三位“善雅数”m=200+10x+y（0≤x≤9，0≤y≤9，x、y为整数），m的各位数字之和为一个完全平方数，求出所有符合条件的“善雅数”中F（m）的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，在△ABC中，∠BAC=90°，AB=AC，点O是BC中点，点D、E分别在BA、AC的延长线上，且OD⊥OE，说明OD=OE．

    查看答案和解析>>

    同步练习册答案