
����Ŀ����ͼ1��ͼ3�У���O��������ABCD�Խ���AC���е㣬��MPNΪֱ�������Σ���MPN��90�㣮������ABCD���ֲ�������MPN������AC����ƽ�ƣ�ƽ�ƹ�����P��ʼ��������AC�ϣ��ұ���PM��ֱ��ֱ��AB�ڵ�E��PN��ֱ��ֱ��BC�ڵ�F��
��1����ͼ1������P���O�غ�ʱ��д��OE��OF��������ϵ��
��2����ͼ2����P���߶�OC��ʱ������OE��OF��������������ϵ��λ�ù�ϵ��������IJ���������֤����
��3����ͼ3������P��AC���ӳ�����ʱ��д��OE��OF��������ϵ��λ�ù�ϵ��
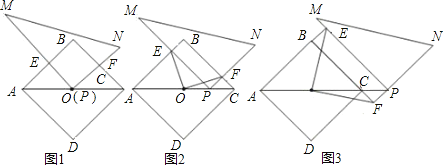
���𰸡���1������������2��OE��OF��OE��OF������������3��OE��OF����ȣ���OE��OF����ֱ�������ɼ�����.
��������
��1���������������ε����ʵó���BAC����BCA��AO��CO���ٸ�����֪�ó���AEO����AFO=90![]() ���Ӷ��õ���AEO����CFO������
���Ӷ��õ���AEO����CFO������
��2����P���߶�OC��ʱ�����������ε�������֤��PF��FC����֤���ı���BEPFΪ���Σ��õ�BE��PF���Ӷ��õ�BE��FC����֤����OBE����OCF������
��3������P��AC���ӳ�����ʱ������ͬ�Ĺ�ϵ����֤�������루2�����ƣ�
��1���⣺������ã�
��BAC����BCA��45�㣬AO��CO��
��AEO����AFO��
����AEO����CFO��
 ��
��
����AEO����CFO��AAS��
��OE��OF��
��2���⣺OE��OF��OE��OF��
֤��������BO��
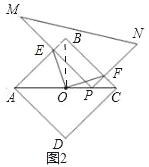
����������ABCD�У�OΪAC�е㣬
��BO��CO��BO��AC����BCA����ABO��45�㣬
��PF��BC����BCO��45�㣬
���FPC��45�㣬PF��FC��
��������ABCD����ABC��90�㣬
��PF��BC��PE��AB��
���PEB����PFB��90�㣮
���ı���PEBF�Ǿ��Σ�
��BE��PF��
��BE��FC��
����OBE����OCF��
��OE��OF����BOE����COF��
�ߡ�COF+��BOF��90�㣬
���BOE+��BOF��90�㣬
���EOF��90�㣮
��OE��OF��
��3��OE��OF����ȣ���OE��OF����ֱ����
���ɣ�����BO��
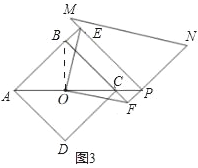
����������ABCD�У�OΪAC�е㣬
��BO��CO��BO��AC����BCA����ABO��45�㣬
���OCF����OBE
��PF��BC����BCO��45�㣬
���FPC��45�㣬PF��FC��
��������ABCD����ABC��90�㣬
��PF��BC��PE��AB��
���PEB����PFB��90�㣮
���ı���PEBF�Ǿ��Σ�
��BE��PF��
��BE��FC��
����OBE����OCF��
��OE��OF����BOE����COF��
�ߡ�COF+��BOF��90�㣬
���BOE+��BOF��90�㣬
���EOF��90�㣮
��OE��OF��


 �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
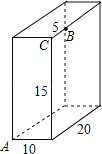
����Ŀ����ͼ��������ij�Ϊ15cm����Ϊ10cm����Ϊ20cm����B���C5cm��һֻ�������Ҫ���ų�����ı���ӵ�A������Bȥ��һ�����ǣ���Ҫ���е���̾����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������� y ax2 2a��x a��0��λ�� x ���Ϸ���ͼ���ΪF1������ x �ύ�� P1��O ���㣬ͼ�� F2��F1����ԭ�� O �Գƣ� F2 �� x �����һ������Ϊ P2 �� F1 ���� F2 ͬʱ�� x ������ƽ�� P1 P2 �ij��ȼ��ɵõ�F3��F4 ���ٽ� F3��F4 ͬʱ�� x ������ƽ�� P1 P2 �ij��ȼ��ɵõ� F5��F6 �������������ķ�ʽһֱƽ����ȥ���ɵõ�һϵ��ͼ�� F1��F2����Fn �����ǰ�����ͼ���Ϊ����������������
��1���� a=��1 ʱ��
���� F1 ͼ��Ķ������ꣻ
�ڵ� H��2014����3�� ���������������������������������������ϣ���ͼ�� F n�Ķ��� T n�ĺ�����Ϊ201����ͼ�� F n��Ӧ�Ľ���ʽΪ �� ���Ա��� x ��ȡֵ��ΧΪ .
��2����ͼ�� Fn��Fn+1 �Ķ���ֱ�Ϊ Tn��Tn+1 ��n Ϊ����������x ����һ�� Q ������Ϊ��12��0������̽���� �� a Ϊ��ֵʱ���� O�� Tn��Tn+1 ��Q �ĵ�Ϊ������ı���Ϊ���Σ���ֱ��д����ʱ n ��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
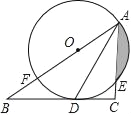
����Ŀ����ͼ����Rt��ABC�У���C��90�㣬ADƽ�֡�BAC����BC�ڵ�D����O��AB�ϣ���O����A��D���㣬��AC�ڵ�E����AB�ڵ�F��
��1����֤��BC����O�����ߣ�
��2������O�İ뾶��2cm��E�ǻ�AD���е㣬����Ӱ���ֵ������������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֱ��l1��y1=![]() x��l2��y2=
x��l2��y2=![]() x��l3��y3=��
x��l3��y3=��![]() x��l4��y4=��
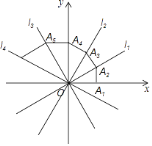
x��l4��y4=��![]() x��OA1=1������A1��A1A2��x�ᣬ��l1�ڵ�A2���ٹ���A2��A2A3��l1��l2�ڵ�A3���ٹ���A3��A3A4��l2��y���ڵ�A4�������A2017����Ϊ________��
x��OA1=1������A1��A1A2��x�ᣬ��l1�ڵ�A2���ٹ���A2��A2A3��l1��l2�ڵ�A3���ٹ���A3��A3A4��l2��y���ڵ�A4�������A2017����Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���ÿ������Ϊ![]() Ԫ��ij����Ʒԭ����ÿ��
Ԫ��ij����Ʒԭ����ÿ��![]() Ԫ���ۣ�һ����۳�
Ԫ���ۣ�һ����۳�![]() �������������г����飬����������Ʒ����ÿ����
�������������г����飬����������Ʒ����ÿ����![]() Ԫ��������������
Ԫ��������������![]() ����
����
![]() ���̳���Ӫ����Ʒԭ��һ��ɻ��������Ԫ��
���̳���Ӫ����Ʒԭ��һ��ɻ��������Ԫ��
![]() ���̳���Ӫ����Ʒһ��Ҫ������
���̳���Ӫ����Ʒһ��Ҫ������![]() Ԫ�����ù˿͵õ�ʵ�ݣ���ÿ����ƷӦ���۶���Ԫ��
Ԫ�����ù˿͵õ�ʵ�ݣ���ÿ����ƷӦ���۶���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪˫����![]() ��ֱ��
��ֱ��![]() ����A��B����,��A������Ϊ(3,2).
����A��B����,��A������Ϊ(3,2).
(1)������ɵ�![]() ��ֵΪ______��
��ֵΪ______��![]() ��ֵΪ________����B������Ϊ_________��
��ֵΪ________����B������Ϊ_________��
(2)ֱ��д����![]() ʱ,
ʱ,![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
(3)����P![]() �ڵ�һ����˫������,�����
�ڵ�һ����˫������,�����![]() ��ֵ����P�����ꡣ
��ֵ����P�����ꡣ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
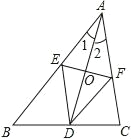
����Ŀ����ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ��߶�AD�Ĵ�ֱƽ���߷ֱ�AB��AC�ڵ�E��F������DE��DF��
(1)���ж��ı���AEDF����״����֤����Ľ��ۣ�
(2)��AE=5��AD=8����EF�ij���
(3)��ABC����ʲô����ʱ���ı���AEDF�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
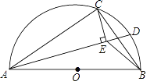
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ������C�ڰ�ԲO�ϣ�AB=5cm��AC=4cm��D�ǻ�BC�ϵ�һ�����㣨���˵�B�������˵�C��������AD������C��CE��AD��E������BE���ڵ�D�ƶ��Ĺ����У�BE��ȡֵ��Χ��____��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com