

 或
或 ,所以分两种情况进行分析;
,所以分两种情况进行分析; 解:(1)当∠POA=90°时,点P运动的路程为⊙O周长的
解:(1)当∠POA=90°时,点P运动的路程为⊙O周长的 或
或 ,
, 时,2π•t=
时,2π•t= •2π•12,
•2π•12, 时,2π•t=
时,2π•t= •2π•12,
•2π•12, 的长为⊙O周长的
的长为⊙O周长的 ,
,

 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
 如图,
如图, |
| AB |
 |
| BC |
A、s=
| ||||
B、s=
| ||||
C、s=
| ||||
D、s=
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•绿园区模拟)如图,⊙O的半径为12,AB是⊙O的弦,并且OD⊥AB于点E,∠AOE=60°,则阴影部分的面积是
(2013•绿园区模拟)如图,⊙O的半径为12,AB是⊙O的弦,并且OD⊥AB于点E,∠AOE=60°,则阴影部分的面积是查看答案和解析>>
科目:初中数学 来源:2007年南京市初中毕业、升学统一考试数学试题 题型:059
如图,A是半径为12 cm的⊙O上的定点,动点P从A出发,以2π cm/s的速度沿圆周逆时针运动,当点P回到A地立即停止运动.

(1)如果∠POA=90°,求点P运动的时间;
(2)如果点B是OA延长线上的一点,AB=OA,那么当点P运动的时间为2 s时,判断直线BP与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源:第28章《圆》中考题集(04):28.1 圆的认识(解析版) 题型:选择题
 圆周,C点是
圆周,C点是 上的任意一点,△ABD是等边三角形,则四边形ABCD的周长P的取值范围是( )
上的任意一点,△ABD是等边三角形,则四边形ABCD的周长P的取值范围是( )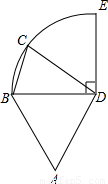
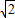

查看答案和解析>>
科目:初中数学 来源:第22章《圆(上)》常考题集(04):22.3 圆的对称性(解析版) 题型:选择题
 圆周,C点是
圆周,C点是 上的任意一点,△ABD是等边三角形,则四边形ABCD的周长P的取值范围是( )
上的任意一点,△ABD是等边三角形,则四边形ABCD的周长P的取值范围是( )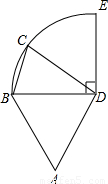
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com