
如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE,交AC于点F.
(1)如图①,当 时,求
时,求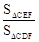 的值;
的值;
(2)如图②当DE平分∠CDB时,求证:AF=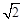 OA;
OA;
(3)如图③,当点E是BC的中点时,过点F作FG⊥BC于点G,求证:CG= BG.
BG.
解:(1)∵ ,∴
,∴ 。
。
∵四边形ABCD是正方形,∴AD∥BC,AD=BC。∴△CEF∽△ADF。
∴ 。∴
。∴ 。∴
。∴ 。
。
(2)证明:∵DE平分∠CDB,∴∠ODF=∠CDF。
又∵AC、BD是正方形ABCD的对角线.∴∠ADO=∠FCD=45°,∠AOD=90°,OA=OD。
又∵∠ADF=∠ADO+∠ODF,∠AFD=∠FCD+∠CDF,∴∠ADF=∠AFD。∴AD=AF。
在Rt△AOD中,根据勾股定理得: ,∴AF=
,∴AF=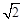 OA。
OA。
(3)证明:连接OE,
∵点O是正方形ABCD的对角线AC、BD的交点,
∴点O是BD的中点。
又∵点E是BC的中点,∴OE是△BCD的中位线。
∴OE∥CD,OE= CD。∴△OFE∽△CFD。
CD。∴△OFE∽△CFD。
∴ 。∴
。∴ 。
。
又∵FG⊥BC,CD⊥BC,∴FG∥CD。∴△EGF∽△ECD。∴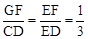 。
。
在Rt△FGC中,∵∠GCF=45°,∴CG=GF。
又∵CD=BC,∴ 。∴
。∴ 。∴CG=
。∴CG= BG。
BG。
解析试题分析:(1)利用相似三角形的性质求得EF于DF的比值,依据△CEF和△CDF同高,则面积的比就是EF与DF的比值,据此即可求解。
(2)利用角之间的关系到证得∠ADF=∠AFD,可以证得AD=AF,在Rt△AOD中,利用勾股定理可以证得。
(3)连接OE,易证OE是△BCD的中位线,然后根据△FGC是等腰直角三角形,易证△EGF∽△ECD,利用相似三角形的对应边的比相等即可证得。


科目:初中数学 来源: 题型:解答题
如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点 )20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?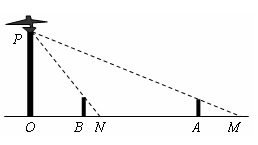
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
一天晚上,黎明和张龙利用灯光下的影子长来测量一路灯D的高度.如图,当李明走到点A处时,张龙测得李明直立时身高AM与影子长AE正好相等;接着李明沿AC方向继续向前走,走到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25m,已知李明直立时的身高为1.75m,求路灯的高CD的长.(结果精确到0.1m).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知,如图, ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1),解答下列问题:
ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1),解答下列问题:
(1)当t为何值时,四边形AQDM是平行四边形?
(2)设四边形ANPM的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使四边形ANPM的面积是 ABCD面积的一半,若存在,求出相应的t值,若不存在,说明理由
ABCD面积的一半,若存在,求出相应的t值,若不存在,说明理由
(4)连接AC,是否存在某一时刻t,使NP与AC的交点把线段AC分成 的两部分?若存在,求出相应的t值,若不存在,说明理由
的两部分?若存在,求出相应的t值,若不存在,说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在△ABC中,∠B=45°,BC=5,高AD=4,矩形EFPQ的一边QP在BC边上,E、F分别在AB、AC上,AD交EF于点H.
(1)求证: ;
;
(2)设EF=x,当x为何值时,矩形EFPQ的面积最大?并求出最大面积;
(3)当矩形EFPQ的面积最大时,该矩形EFPQ以每秒1个单位的速度沿射线DA匀速向上运动(当矩形的边PQ到达A点时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,求S与t的函数关系式,并写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在Rt△ABC,∠C=90°,D为AB边上一点,点M、N分别在BC、AC边上,且DM⊥DN.作MF⊥AB于点F,NE⊥AB于点E.
(1)特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;
(2)拓展探究:若AC≠BC.
①如图2,若D为AB中点,(1)中的两个结论有一个仍成立,请指出并加以证明;
②如图3,若BD=kAD,条件中“点M在BC边上”改为“点M在线段CB的延长线上”,其它条件不变,请探究AE与DF的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D地边AC上,点E、F在边AB上,点G在边BC上。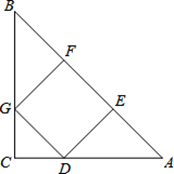
(1)求证:△ADE≌△BGF;
(2)若正方形DEFG的面积为16cm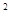 ,求AC的长。
,求AC的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com