
【题目】如图,在平面直角坐标系xoy中,抛物线![]() 与
与![]() 轴交于点A(-3,0),C(1,0),与
轴交于点A(-3,0),C(1,0),与![]() 轴交于点B.
轴交于点B.
(1)求此抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A,B重合),过点P作![]() 轴的垂线,垂足交点为F,交直线AB于点E,作
轴的垂线,垂足交点为F,交直线AB于点E,作![]() 于点D.
于点D.
①点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;
②连接PA,以PA为边作正方形APMN,当顶点M或N恰好落在抛物线对称轴上时,求出对应的P点的坐标.
【答案】(1) ![]() ;
;
(2) ①P(-![]() );②P(-
);②P(-![]() -1,2).
-1,2).
【解析】分析:(1)把点A、C的坐标代入抛物线解析式,利用待定系数法求二次函数解析式解答即可;
(2)①根据点A、B的坐标求出OA=OB,从而得到△AOB是等腰直角三角形,根据等腰直角三角形的性质可得∠BAO=45°,然后求出△PED是等腰直角三角形,根据等腰直角三角形的性质,PD越大,△PDE的周长最大,再判断出当与直线AB平行的直线与抛物线只有一个交点时,PD最大,再求出直线AB的解析式为y=x+3,设与AB平行的直线解析式为y=x+m,与抛物线解析式联立消掉y,得到关于x的一元二次方程,利用根的判别式△=0列式求出m的值,再求出x、y的值,从而得到点P的坐标;
②先确定出抛物线的对称轴,然后(i)分点M在对称轴上时,过点P作PQ⊥对称轴于Q,根据同角的余角相等求出∠APF=∠QPM,再利用“角角边”证明△APF和△MPQ全等,根据全等三角形对应边相等可得PF=PQ,设点P的横坐标为n,表示出PQ的长,即PF,然后代入抛物线解析式计算即可得解;(ii)点N在对称轴上时,同理求出△APF和△ANQ全等,根据全等三角形对应边相等可得PF=AQ,根据点A的坐标求出点P的纵坐标,再代入抛物线解析式求出横坐标,即可得到点P的坐标.
详解:解:(1)∵抛物线y=ax2+bx+3经过点A(-3,0),C(1,0),
∴![]() ,解得
,解得![]() ,
,
所以,抛物线的解析式为y=-x2-2x+3;
(2)①∵A(-3,0),B(0,3),
∴OA=OB=3,
∴△AOB是等腰直角三角形,
∴∠BAO=45°,
∵PF⊥x轴,
∴∠AEF=90°-45°=45°,
又∵PD⊥AB,
∴△PDE是等腰直角三角形,
∴PD越大,△PDE的周长越大,
易得直线AB的解析式为y=x+3,
设与AB平行的直线解析式为y=x+m,
联立![]() ,
,
消掉y得,x2+3x+m-3=0,
当△=32-4×1×(m-3)=0,
即m=![]() 时,直线与抛物线只有一个交点,PD最长,
时,直线与抛物线只有一个交点,PD最长,
此时x=-![]() ,y=-
,y=-![]() +
+![]() =
=![]() ,
,
∴点P(-![]() ,
,![]() )时,△PDE的周长最大;
)时,△PDE的周长最大;
②抛物线y=-x2-2x+3的对称轴为直线x=-![]() =-1,
=-1,
(i)如图1,点M在对称轴上时,过点P作PQ⊥对称轴于Q,
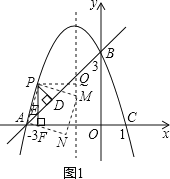
在正方形APMN中,AP=PM,∠APM=90°,
∴∠APF+∠FPM=90°,∠QPM+∠FPM=90°,
∴∠APF=∠QPM,
∵在△APF和△MPQ中,
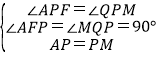 ,
,
∴△APF≌△MPQ(AAS),
∴PF=PQ,
设点P的横坐标为n(n<0),则PQ=-1-n,
即PF=-1-n,
∴点P的坐标为(n,-1-n),
∵点P在抛物线y=-x2-2x+3上,
∴-n2-2n+3=-1-n,
整理得,n2+n-4=0,
解得n1=![]() (舍去),n2=
(舍去),n2=![]() ,
,
-1-n=-1-![]() =
=![]() ,
,
所以,点P的坐标为(![]() ,
,![]() );
);
(ii)如图2,点N在对称轴上时,设抛物线对称轴与x轴交于点Q,

∵∠PAF+∠FPA=90°,∠PAF+∠QAN=90°,
∴∠FPA=∠QAN,
又∵∠PFA=∠AQN=90°,PA=AN,
∴△APF≌△NAQ,
∴PF=AQ,
设点P坐标为P(x,-x2-2x+3),
则有-x2-2x+3=-1-(-3)=2,
解得x=![]() -1(不合题意,舍去)或x=-
-1(不合题意,舍去)或x=-![]() -1,
-1,
此时点P坐标为(-![]() -1,2).
-1,2).
综上所述,当顶点M恰好落在抛物线对称轴上时,点P坐标为(![]() ,
,![]() ),当顶点N恰好落在抛物线对称轴上时,点P的坐标为(-
),当顶点N恰好落在抛物线对称轴上时,点P的坐标为(-![]() -1,2).
-1,2).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】材料一:我们可以将任意三位数记为![]() ,(其中
,(其中![]() 、
、![]() 、
、![]() 分别表示该数的百位数字,十位数字和个位数字,且
分别表示该数的百位数字,十位数字和个位数字,且![]() ).显然
).显然![]() .
.
材料二:若一个三位数的百位数字,十位数字和个位数字均不为![]() ,则称之为“生数”,比如
,则称之为“生数”,比如![]() 就是一个“生数”,将“生数”的三个数位上的数字交换顺序,可产生出
就是一个“生数”,将“生数”的三个数位上的数字交换顺序,可产生出![]() 个新的“生数”,比如由
个新的“生数”,比如由![]() 可以产生出
可以产生出![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这
这![]() 个新“生数”,将这
个新“生数”,将这![]() 个数相加,得到的和
个数相加,得到的和![]() 称为由“生数”
称为由“生数”![]() 生成的“完全数”
生成的“完全数”
问题:(1)求证:任意一个“完全数”都可以整除![]() ;
;
(2)若一个四位正整数![]() (
(![]() ,
,![]() 是整数)是由一个“生数”
是整数)是由一个“生数”![]() (
(![]() ,
,![]() ,
, ![]() 、
、![]() 是整数)产生的“完全数”,请求出这个“生数”
是整数)产生的“完全数”,请求出这个“生数”![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
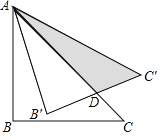
【题目】如图,等腰直角三角形ABC的直角边AB的长为![]() ,将△ABC绕点A逆时针旋转15°后得到△AB′C′,AC与B′C′相交于点D,则图中阴影△ADC′的面积等于______.
,将△ABC绕点A逆时针旋转15°后得到△AB′C′,AC与B′C′相交于点D,则图中阴影△ADC′的面积等于______.
查看答案和解析>>
科目:初中数学 来源: 题型:
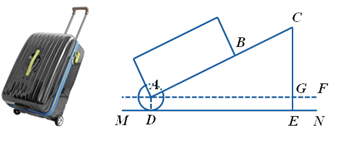
【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示.已知箱体长AB=50cm,拉杆![]() 的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
设AF∥MN.
(1)求⊙A的半径长;
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服.某人将手自然下垂在C端拉旅行箱时,CE为80cm,![]() =64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:
=64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点,已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An.
(1)若点A1的坐标为(2,1),则点A4的坐标为_____;
(2)若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:在“![]() ”中的每个□内,填入
”中的每个□内,填入![]() 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若请推算![]() □内的符号;
□内的符号;
(3)在“![]() ”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,抛物线y=﹣![]() x2﹣
x2﹣![]() x+3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,点D的坐标是(0,﹣1),连接BC、AC
x+3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,点D的坐标是(0,﹣1),连接BC、AC

(1)求出直线AD的解析式;
(2)如图2,若在直线AC上方的抛物线上有一点F,当△ADF的面积最大时,有一线段MN=![]() (点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF,请求出四边形AMNF的周长最小时点N的横坐标;
(点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF,请求出四边形AMNF的周长最小时点N的横坐标;
(3)如图3,将△DBC绕点D逆时针旋转α°(0<α°<180°),记旋转中的△DBC为△DB′C′,若直线B′C′与直线AC交于点P,直线B′C′与直线DC交于点Q,当△CPQ是等腰三角形时,求CP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系中放入一个边长AB长为3,BC长为5的矩形纸片ABCD,使得BC、AB所在直线分别与x、y轴重合.将纸片沿着折痕AE翻折后,点D恰好落在x轴上,记为F.

(1)求折痕AE所在直线与x轴交点的坐标;
(2)如图2,过D作DG⊥AF,求DG的长度;
(3)将矩形ABCD水平向右移动n个单位,则点B坐标为(n,0),其中n>0.如图3所示,连接OA,若△OAF是等腰三角形,试求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次测绘活动中,某同学站在点A处观测停放于B、C两处的小船,测得船B在点A北偏东75°方向150米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为______米(精确到0.1![]() ).
).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com