
 如图,抛物线y=-x2+bx+c经过点A(1,0),C(4,0),与y轴交于点B.
如图,抛物线y=-x2+bx+c经过点A(1,0),C(4,0),与y轴交于点B.分析 (1)利用待定系数法即可求得抛物线的解析式;
(2)首先求得B的坐标则AB的长即可求得,根据AB是腰,即可求得P的坐标.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{-1+b+c=0}\\{-16+4b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=5}\\{c=-4}\end{array}\right.$,
则抛物线的解析式是y=-x2+5x-4;
(2)在y=-x2+5x-4中,令x=0,解得y=-4,
则B的坐标是(0,-4).
则AB=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,
当A是等腰三角形的顶角顶点时,AP=AB,此时P与B关于x轴对称,则坐标是(0,4);
当B是等腰三角新的顶点时,BP=BA,则OP=$\sqrt{17}$-4,P的坐标是(0,$\sqrt{17}$-4).
总之,P的坐标是(0,$\sqrt{17}$-4)或(0,4).
点评 本题考查了待定系数法求函数解析式,正确进行讨论是关键.


科目:初中数学 来源: 题型:选择题
| 砝码的质量x(克) | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 | 600 |
| 弹簧的长度y(厘米) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.5 | 7.5 |
| A. | 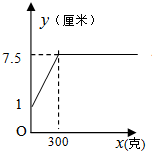 | B. | 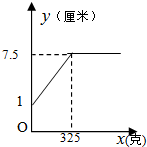 | ||
| C. | 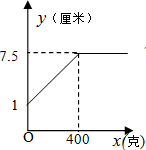 | D. | 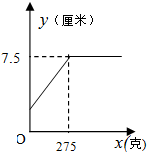 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
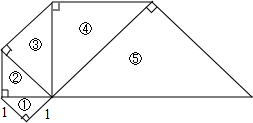 一系列等腰直角三角形组成的螺旋形如图所示,其序号依次为①,②,③,④,⑤,…,则第n等腰直角三角形的斜边长为($\sqrt{2}$)n.
一系列等腰直角三角形组成的螺旋形如图所示,其序号依次为①,②,③,④,⑤,…,则第n等腰直角三角形的斜边长为($\sqrt{2}$)n.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
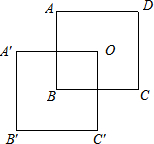 将大小相同的两个正方形纸片按如图所示方式叠放在一起,已知正方形的边长为2,点O为正方形的中心,至少平移几个单位长度才能使两个正方形完全重合?( )
将大小相同的两个正方形纸片按如图所示方式叠放在一起,已知正方形的边长为2,点O为正方形的中心,至少平移几个单位长度才能使两个正方形完全重合?( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com