
��ƽ��ֱ������ϵxOy�У�OΪ����ԭ�㣩����֪������y=x2+bx+c����A��4��0����B��1����3����
��1����b��c��ֵ����д���������ߵĶԳ���Ͷ������ꣻ
��2���������ߵĶԳ���Ϊֱ��l����P��m��n�������������ڵ�һ���ĵ㣬��E���P����ֱ��l�Գƣ���E���F����y��Գƣ����ı���OAPF�����Ϊ48�����P�����ꣻ
��3���ڣ�2���������£���M��ֱ��l������һ�㣬���ж�MP+MA�Ƿ������Сֵ�������ڣ���������Сֵ����Ӧ�ĵ�M�����ꣻ�������ڣ���˵�����ɣ�
��1��b=��4��c=0�������ߵĶԳ���Ϊx=2������Ϊ��2����4����
��2����P��������6��12����
��3�����ڣ���СֵΪ6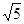 ��
��
���������������1���ô���ϵ�����Ϳ����b��c���ٽ�����ʽ��ɶ���ʽ���Ϳ����ˣ�
��2��������֪�����ɵ�E��4��m��n����F��m��4��n�����Ӷ��õ�PF=4�������ı���OAPF�����Ϊ48�������P�������꣬Ȼ����������ߵĽ���ʽ�Ϳ������P�����꣮
��3�����ݵ�E���P����ֱ��l�Գƿɵ�MP=ME������MP+MA=ME+MA�����ɡ�����֮���߶���̡��ɵ�AE�ij�����MP+MA����Сֵ�����ù��ɶ����Ϳɽ�����⣮
�����������1����������y=x2+bx+c����A��4��0����B��1����3����
��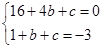 ��
��
��ã�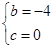 ��
��
��y=x2��4x=��x��2��2��4��
�������ߵĶԳ���Ϊx=2������Ϊ��2����4����
��2����ͼ1��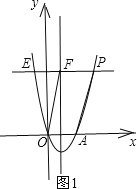
�ߵ�P��m��n�����E����ֱ��x=2�Գƣ�
���E��������4��m��n����
�ߵ�E���F����y��Գƣ�
���F��������m��4��n����
��PF=m����m��4��=4��
��PF=OA=4��
��PF��OA��
���ı���OAPF��ƽ���ı��Σ�
��S?OAPF=OA•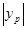 =4n=48��
=4n=48��
��n=12��
��m2��4m=n=12��
��ã�m1=6��m2=��2��
�ߵ�P�����������ڵ�һ���ĵ㣬
��m=6��
���P��������6��12����
��3������E��EH��x�ᣬ����ΪH����ͼ2��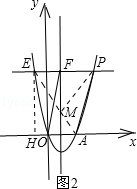
�ڣ�2���������£���P��6��12����E����2��12����
��AH=4������2��=6��EH=12��
��EH��x�ᣬ����EHA=90�㣬
��EA2=EH2+AH2=122+62=180��
��EA=6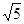 ��
��
�ߵ�E���P����ֱ��l�Գƣ�
��MP=ME��
��MP+MA=ME+MA��
���ݡ�����֮���߶���̡��ɵã�
����E��M��A����ʱ��MP+MA��С����Сֵ����EA�ij�����6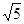 ��
��
���㣺1������ϵ������2���߶ε����ʣ�3�����ɶ�����4������x�ᡢy��ԳƵĵ�����꣮.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ֱ֪��y=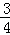 x��3��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=��
x��3��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=��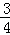 x2+mx+n������A�͵�C��
x2+mx+n������A�͵�C��
��1����������ߵĽ���ʽ��
��2����ֱ��CA�Ϸ������������Ƿ���ڵ�D��ʹ�á�ACD�������������ڣ������D�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У���֪��O��0��0����A��5��0����B��4��4����
��1�����O��B��A����������ߵĽ���ʽ��
��2���ڵ�һ�����������ϴ��ڵ�M��ʹ��O��A��B��MΪ������ı������������M�����꣮
��3����ֱ��x=m���������ڵ�P�����߶�OB�ڵ�Q������PQBΪ����������ʱ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ1����ƽ��ֱ������ϵxOy�У���MΪ������ �Ķ��㣬���㣨0��4����x���ƽ���ߣ����������ڵ�P��Q����P��Q����ࣩ��PQ=4��
�Ķ��㣬���㣨0��4����x���ƽ���ߣ����������ڵ�P��Q����P��Q����ࣩ��PQ=4��
��1���������ߵĺ�����ϵʽ����д����P�����ꣻ
��2��С�����֣��������� ���ŵ�P��ת180�㣬�����������ߵĶ���ǡΪ����ԭ��O������Ϊ��ȷ����˵�����ɣ�
���ŵ�P��ת180�㣬�����������ߵĶ���ǡΪ����ԭ��O������Ϊ��ȷ����˵�����ɣ�
��3����ͼ2����֪��A��1��0������PAΪ��������PABC����P��A��B��C��˳ʱ��ķ������У��� ��
��
��д��C������꣺C�� �� ���������ú���t�Ĵ���ʽ��ʾ����
������C���⣨2������ת������������ϣ���t��ֵ��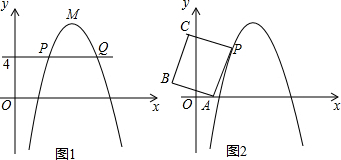
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪������y=3ax2+2bx+c
��1����a=b=1��c=-1�����������x��Ľ������ꣻ
��2����a=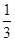 ��c=2+b����������
��c=2+b����������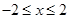 �����ϵ���Сֵ��-3����b��ֵ��
�����ϵ���Сֵ��-3����b��ֵ��
��3����a+b+c=1���Ƿ����ʵ��x��ʹ����Ӧ��y��ֵΪ1����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ1��2����֪�ı���ABCDΪ�����Σ�������AC����һ����P����PE��AD�����ӳ��ߣ���E����PF��DC�����ӳ��ߣ���F��������BP��EF��G��
��1����ͼ1�У���������ABCD�ı߳�Ϊ2���ı���ABFE�����Ϊy��AP=x����y����x�ĺ�������ʽ��
��2�����ۣ�GB��EF��ͼ1��ͼ2���dz����ģ�����ѡһͼ�θ���֤����
��3�������ͼ2֤������FGC�ס�PFB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪������y=ax2+bx+c��x���һ������ΪA��3��0������y��Ľ���ΪB��0��3�����䶥��ΪC���Գ���Ϊx=1��
��1���������ߵĽ���ʽ��
��2����֪��MΪy���ϵ�һ�����㣬����ABMΪ����������ʱ�����M�����ꣻ
��3������AOB��x������ƽ��m����λ���ȣ�0��m��3���õ���һ�������Σ������õ����������ABC�ص����ֵ������ΪS����m�Ĵ���ʽ��ʾS��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
������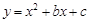 ��b��c��Ϊ��������x�ύ��
��b��c��Ϊ��������x�ύ��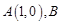 ���㣬��y�ύ�ڵ�
���㣬��y�ύ�ڵ� ��
��
��1����������߶�Ӧ�ĺ�������ʽ��
��2����P����������һ�㣬�ҵ�P�������ߵĶԳ���ľ���Ϊ3����ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com