
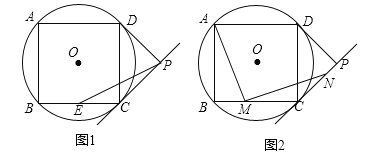
【题目】如图,四边形ABCD是⊙O的内接正方形,AB=4,PC、PD是⊙O的两条切线,C、D为切点.
(1)如图1,求⊙O的半径;
(2)如图1,若点E是BC的中点,连接PE,求PE的长度;
(3)如图2,若点M是BC边上任意一点(不含B、C),以点M为直角顶点,在BC的上方作∠AMN=90°,交直线CP于点N,求证:AM=MN.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见试题解析.
;(3)证明见试题解析.
【解析】
试题分析:(1)由切线的性质和正方形的判定与性质得出⊙O的半径即可;
(2)由垂径定理得出OE⊥BC,∠OCE=45°,再用勾股定理即可得出结论;
(3)在AB上截取BF=BM,利用(1)中所求,得出∠ECP=135°,再利用全等三角形的判定与性质得出即可.
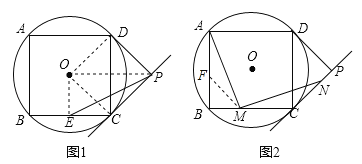
试题解析:(1)如图1,连接OD,OC,∵PC、PD是⊙O的两条切线,C、D为切点,∴∠ODP=∠OCP=90°,∵四边形ABCD是⊙O的内接正方形,∴∠DOC=90°,OD=OC,∴四边形DOCP是正方形,∵AB=4,∠ODC=∠OCD=45°,∴DO=CO=DCsin45°=![]() ×4=
×4=![]() ;
;
(2)如图1,连接EO,OP,∵点E是BC的中点,∴OE⊥BC,∠OCE=45°,则∠E0P=90°,∴EO=EC=2,OP=![]() CO=4,∴PE=
CO=4,∴PE=![]() =
=![]() ;
;
(3)如图2,在AB上截取BF=BM,∵AB=BC,BF=BM,∴AF=MC,∠BFM=∠BMF=45°,∵∠AMN=90°,∴∠AMF+∠NMC=45°,∠FAM+∠AMF=45°,∴∠FAM=∠NMC,∵由(1)得:PD=PC,∠DPC=90°,∴∠DCP=45°,∴∠MCN=135°,∵∠AFM=180°﹣∠BFM=135°,在△AFM和△CMN中,∵∠FAM=∠CMN,AF=MC,∠AFM=∠MCN,∴△AFM≌△CMN(ASA),∴AM=MN.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,三个内角的平分线AD、BM、CN交于点O,OE⊥BC于点E.
(1)求∠ABO+∠BCO+∠CAO的度数;
(2)∠BOD与∠COE是否相等?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】供电局的电力维修工要到30千米远的郊区进行电力抢修.技术工人骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果他们同时到达.已知抢修车的速度是摩托车的1.5倍,求这两种车的速度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上全班男生进行了百米测试,达标成绩为14秒,下面是第一小组8名男生的成绩记录,其中“+”表示成绩大于14秒,“﹣”表示成绩小于14秒
﹣1 | +0.8 | 0 | ﹣1.2 | ﹣0.1 | 0 | +0.5 | ﹣0.6 |
(1)求这个小组的男生达标率是多少?
(2)求这个小组8名男生的平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校随机抽取部分学生,就“学习习惯”进行调查,将“对自己做错题进行整理、分析、改正”(选项为:很少、有时、常常、总是)的调查数据进行了整理,绘制成部分统计图如下: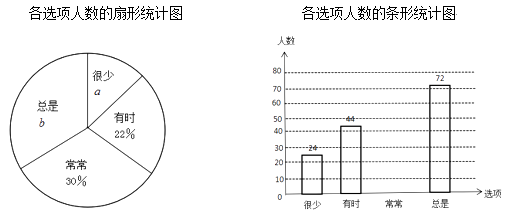
请根据图中信息,解答下列问题:
(1)该调查的样本容量为 , ![]() =%,
=%, ![]() =%,“常常”对应扇形的圆心角的度数为;
=%,“常常”对应扇形的圆心角的度数为;
(2)请你补全条形统计图;
(3)若该校有3200名学生,请你估计其中“总是”对错题进行整理、分析、改正的
学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强公民的节水意识,合理利用水资源.某市对居民用水实行阶梯水价,居民家庭每月用水量划分为三个阶梯,一、二、三级阶梯用水的单价之比等于1:1.5:2.如图折线表示实行阶梯水价后每月水费y(元)与用水量xm3之间的函数关系.其中线段AB表示第二级阶梯时y与x之间的函数关系.
(1)写出点B的实际意义;
(2)求线段AB所在直线的表达式;
(3)某户5月份按照阶梯水价应缴水费102元,其相应用水量为多少立方米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com