
【题目】如图,菱形![]() 的边长为1,
的边长为1,![]() ,点E是边
,点E是边![]() 上任意一点(端点除外),线段
上任意一点(端点除外),线段![]() 的垂直平分线交
的垂直平分线交![]() ,
,![]() 分别于点F,G,
分别于点F,G,![]() ,
,![]() 的中点分别为M,N.
的中点分别为M,N.
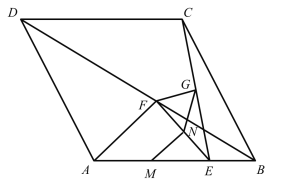
(1)求证:![]() ;
;
(2)求![]() 的最小值;
的最小值;
(3)当点E在![]() 上运动时,
上运动时,![]() 的大小是否变化?为什么?
的大小是否变化?为什么?
【答案】(1)见解析;(2)![]() ;(3)不变,理由见解析.
;(3)不变,理由见解析.
【解析】
(1)连接CF,根据垂直平分线的性质和菱形的对称性得到CF=EF和CF=AF即可得证;
(2)连接AC,根据菱形对称性得到AF+CF最小值为AC,再根据中位线的性质得到MN+NG的最小值为AC的一半,即可求解;
(3)延长EF,交DC于H,利用外角的性质证明∠AFC=∠FCE+∠FEC+∠FAE+∠FEA,再由AF=CF=EF,得到∠AEF=∠EAF,∠FEC=∠FCE,从而推断出∠AFD=∠FAE+∠ABF=∠FAE+∠CEF,从而可求出∠ABF=∠CEF=30°,即可证明.
解:(1)连接CF,
∵FG垂直平分CE,
∴CF=EF,
∵四边形ABCD为菱形,
∴A和C关于对角线BD对称,
∴CF=AF,
∴AF=EF;
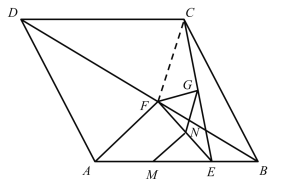
(2)连接AC,
∵M和N分别是AE和EF的中点,点G为CE中点,
∴MN=![]() AF,NG=
AF,NG=![]() CF,即MN+NG=
CF,即MN+NG=![]() (AF+CF),
(AF+CF),
当点F与菱形ABCD对角线交点O重合时,
AF+CF最小,即此时MN+NG最小,
∵菱形ABCD边长为1,∠ABC=60°,
∴△ABC为等边三角形,AC=AB=1,
即MN+NG的最小值为![]() ;
;
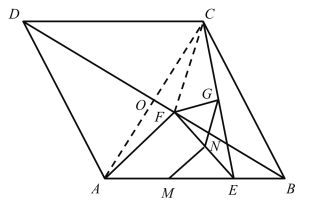
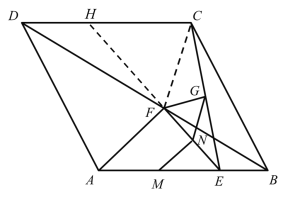
(3)不变,理由是:
延长EF,交DC于H,
∵∠CFH=∠FCE+∠FEC,∠AFH=∠FAE+∠FEA,
∴∠AFC=∠FCE+∠FEC+∠FAE+∠FEA,
∵点F在菱形ABCD对角线BD上,根据菱形的对称性可得:
∠AFD=∠CFD=![]() ∠AFC,
∠AFC,
∵AF=CF=EF,
∴∠AEF=∠EAF,∠FEC=∠FCE,
∴∠AFD=∠FAE+∠ABF=∠FAE+∠CEF,
∴∠ABF=∠CEF,
∵∠ABC=60°,
∴∠ABF=∠CEF=30°,为定值.


科目:初中数学 来源: 题型:
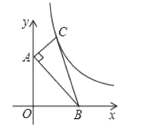
【题目】如图,在平面直角坐标系中,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,点
,点![]() 在第一象限内,
在第一象限内,![]() ,
,![]() ,函数
,函数![]() 的图像经过点
的图像经过点![]() ,将
,将![]() 沿
沿![]() 轴的正方向向右平移
轴的正方向向右平移![]() 个单位长度,使点
个单位长度,使点![]() 恰好落在函数
恰好落在函数![]() 的图像上,则
的图像上,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.3D.
C.3D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园的门票价格如表:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
现某单位要组织其市场部和生产部的员工游览该公园,这两个部门人数分别为a和b(a≥b).若按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;若两个部门合在一起作为一个团体,同一时间购票游览公园,则共需支付门票费为990元,那么这两个部门的人数a=_____;b=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,观测站C发现在它的正西方向,有一艘渔船B出现险情,需救援,当即上报救援中心A,测得C在A的南偏东67方向,距A处50海里,而B在A的南偏东30方向,求渔船B与救援中心A的距离AB,渔船B与观测站C的距离BC.(结果精确到0.1海里)(参考数据:sin37=0.6,cos37=0.8,tan37=![]() ,
,![]() ≈1.73)
≈1.73)
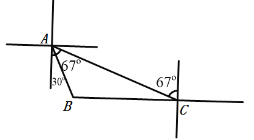
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年是脱贫攻坚年,为实现全员脱贫目标,某村贫困户在当地政府支持帮助下,办起了养鸡场,经过一段时间精心饲养,总量为3000只的一批鸡可以出售.现从中随机抽取50只,得到它们质量的统计数据如下:
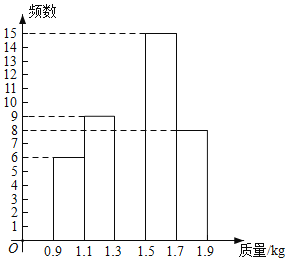
质量 | 组中值 | 数量(只) |
| 1.0 | 6 |
| 1.2 | 9 |
| 1.4 | a |
| 1.6 | 15 |
| 1.8 | 8 |
根据以上信息,解答下列问题:
(1)表中![]() ______,补全频数分布直方图;
______,补全频数分布直方图;
(2)这批鸡中质量不小于![]() 的大约有多少只?
的大约有多少只?
(3)这些贫因户的总收入达到54000元,就能实现全员脱贫目标.按15元![]() 的价格售出这批鸡后,该村贫困户能否脱贫?
的价格售出这批鸡后,该村贫困户能否脱贫?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AB是![]() 的直径,点C是
的直径,点C是![]() 上一点,连接AC、BC,直线MN过点C,满足
上一点,连接AC、BC,直线MN过点C,满足![]() .
.
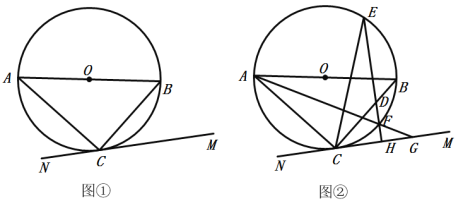
(1)如图①,求证:直线MN是![]() 的切线;
的切线;
(2)如图②,点D在线段BC上,过点D作![]() 于点H,直线DH交
于点H,直线DH交![]() 于点E、F,连接AF并延长交直线MN于点G,连接CE,且
于点E、F,连接AF并延长交直线MN于点G,连接CE,且![]() ,若
,若![]() 的半径为1,
的半径为1,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
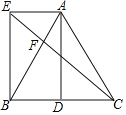
【题目】如图,在△ABC中,AB=AC,D为BC中点,AE∥BD,且AE=BD.
(1)求证:四边形AEBD是矩形;
(2)连接CE交AB于点F,若∠ABE=30°,AE=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接:“国家卫生城市”复检,某市坏卫局准备购买A、B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元,购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.
(1)求每个A型垃圾箱和B型垃圾箱各多少元?
(2)该市现需要购A、B买两种型号的垃圾箱共30个,其中买A型垃圾箱不超过16个.求出购买费用最少时的购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
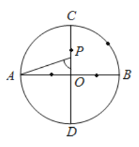
【题目】如图,![]() 是
是![]() 的两条互相垂直的直径,点P从点O出发,沿
的两条互相垂直的直径,点P从点O出发,沿![]() 的路线匀速运动,设
的路线匀速运动,设![]() (单位:度),那么y与点P运动的时间(单位:秒)的关系图是( )
(单位:度),那么y与点P运动的时间(单位:秒)的关系图是( )
A.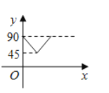 B.
B.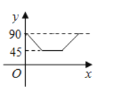 C.
C.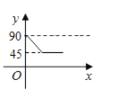 D.
D.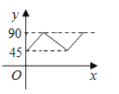
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com