
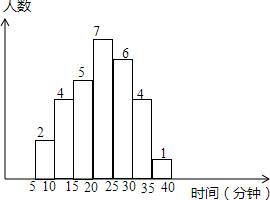
 一个学习小组对某生双休日在家参加家务劳动所用的大致时间(以整数计)作了抽样调查,结合图中信息,则这个小组所抽取样本的容量是29.
一个学习小组对某生双休日在家参加家务劳动所用的大致时间(以整数计)作了抽样调查,结合图中信息,则这个小组所抽取样本的容量是29.  口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
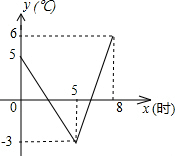 由于冷空气的入侵,地面气温急剧下降到0℃以下的天气现象称为“霜冻”,某种植物在气温是0℃以下的时间超过3小时,即遭受霜冻灾害,需采取预防措施.下图是气象台某天发布的该地区气象信息,预报了次日0时~8时气温随时间变化情况,其中0时~5时,5时~8时的图象分别满足一次函数关系.根据图中信息:
由于冷空气的入侵,地面气温急剧下降到0℃以下的天气现象称为“霜冻”,某种植物在气温是0℃以下的时间超过3小时,即遭受霜冻灾害,需采取预防措施.下图是气象台某天发布的该地区气象信息,预报了次日0时~8时气温随时间变化情况,其中0时~5时,5时~8时的图象分别满足一次函数关系.根据图中信息:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com