
”¾ĢāÄæ”æČēĶ¼ŹĒĪŅ¹ś¹Å“śŹżŃ§¼ŅŃī»Ō×īŌē·¢Ļֵģ¬³ĘĪŖ”°Ńī»ŌČż½Ē”±£®ĖüµÄ·¢ĻÖ±ČĪ÷·½ŅŖŌēĪå°ŁÄź×óÓŅ£¬ÓÉ“ĖæɼūĪŅ¹ś¹Å“śŹżŃ§µÄ³É¾ĶŹĒ·Ē³£ÖµµĆÖŠ»ŖĆń×å×ŌŗĄµÄ£””°Ńī»ŌČż½Ē”±ÖŠÓŠŠķ¶ą¹ęĀÉ£¬ČēĖüµÄĆæŅ»ŠŠµÄŹż×ÖÕżŗƶŌÓ¦ĮĖ£Øa+b£©n£ØnĪŖ·ĒøŗÕūŹż£©µÄÕ¹æŖŹ½ÖŠa°““ĪŹż“ӓ󵽊”ÅÅĮŠµÄĻīµÄĻµŹż£®ĄżČē£¬£Øa+b£©2£½a2+2ab+b2Õ¹æŖŹ½ÖŠµÄĻµŹż1”¢2”¢1Ē”ŗƶŌÓ¦Ķ¼ÖŠµŚČżŠŠµÄŹż×Ö£»ŌŁČē£¬£Øa+b£©3£½a3+3a2b+3ab2+b3Õ¹æŖŹ½ÖŠµÄĻµŹż1”¢3”¢3”¢1Ē”ŗƶŌÓ¦Ķ¼ÖŠµŚĖÄŠŠµÄŹż×Ö£®ĒėČĻÕę¹Ū²ģ“ĖĶ¼£¬Š“³ö£Øa©b£©4µÄÕ¹æŖŹ½£¬£Øa©b£©4£½_____£®

”¾“š°ø”æa4©4a3b+6a2b2©4ab3+b4
”¾½āĪö”æ
ÓÉ£Øa+b£©=a+b£¬£Øa+b£©2=a2+2ab+b2£¬£Øa+b£©3=a3+3a2b+3ab2+b3æÉµĆ£Øa+b£©nµÄø÷ĻīÕ¹æŖŹ½µÄĻµŹż³żŹ×Ī²Į½Ļī¶¼ŹĒ1Ķā£¬ĘäÓąø÷ĻīĻµŹż¶¼µČÓŚ£Øa+b£©n-1µÄĻąĮŚĮ½øöĻµŹżµÄŗĶ£¬ÓÉ“ĖæÉµĆ£Øa”Ąb£©4µÄø÷ĻīĻµŹżŅĄ“ĪĪŖ1”¢4”¢6”¢4”¢1£®
½ā£ŗ£Øa©b£©4£½a4©4a3b+6a2b2©4ab3+b4£®
¹Ź“š°øĪŖ£ŗa4©4a3b+6a2b2©4ab3+b4£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬Å×ĪļĻß![]() µÄ¶„µćĪŖµć
µÄ¶„µćĪŖµć![]() £¬Óė
£¬Óė![]() ÖįµÄøŗ°ėÖį½»ÓŚµć
ÖįµÄøŗ°ėÖį½»ÓŚµć![]() £¬Ö±Ļß
£¬Ö±Ļß![]() ½»Å×ĪļĻßWÓŚĮķŅ»µć
½»Å×ĪļĻßWÓŚĮķŅ»µć![]() £¬µć
£¬µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() £®
£®
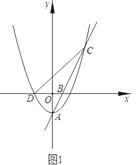
£Ø1£©ĒóÖ±Ļß![]() µÄ½āĪöŹ½£»
µÄ½āĪöŹ½£»
£Ø2£©¹żµć![]() ×÷
×÷![]() Öį£¬½»
Öį£¬½»![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬Čō
£¬Čō![]() Ę½·Ö
Ę½·Ö![]() £¬ĒóÅ×ĪļĻßWµÄ½āĪöŹ½£»
£¬ĒóÅ×ĪļĻßWµÄ½āĪöŹ½£»
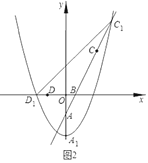
£Ø3£©Čō![]() £¬½«Å×ĪļĻßWĻņĻĀĘ½ŅĘ
£¬½«Å×ĪļĻßWĻņĻĀĘ½ŅĘ![]() øöµ„Ī»µĆµ½Å×ĪļĻß
øöµ„Ī»µĆµ½Å×ĪļĻß![]() £¬ČēĶ¼2£¬¼ĒÅ×ĪļĻß
£¬ČēĶ¼2£¬¼ĒÅ×ĪļĻß![]() µÄ¶„µćĪŖ
µÄ¶„µćĪŖ![]() £¬Óė
£¬Óė![]() Öįøŗ°ėÖįµÄ½»µćĪŖ
Öįøŗ°ėÖįµÄ½»µćĪŖ![]() £¬ÓėÉäĻß
£¬ÓėÉäĻß![]() µÄ½»µćĪŖ
µÄ½»µćĪŖ![]() £®ĪŹ£ŗŌŚĘ½ŅĘµÄ¹ż³ĢÖŠ£¬
£®ĪŹ£ŗŌŚĘ½ŅĘµÄ¹ż³ĢÖŠ£¬![]() ŹĒ·ńŗćĪŖ¶ØÖµ£æČōŹĒ£¬ĒėĒó³ö
ŹĒ·ńŗćĪŖ¶ØÖµ£æČōŹĒ£¬ĒėĒó³ö![]() µÄÖµ£»Čō²»ŹĒ£¬ĒėĖµĆ÷ĄķÓÉ£®
µÄÖµ£»Čō²»ŹĒ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬·“±ČĄżŗÆŹży£½![]() £Øx£¾0£©ŗĶŅ»“ĪŗÆŹży£½mx+nµÄĶ¼Ļó¹żøńµć£ØĶųøńĻߵĽ»µć£©B”¢P£®
£Øx£¾0£©ŗĶŅ»“ĪŗÆŹży£½mx+nµÄĶ¼Ļó¹żøńµć£ØĶųøńĻߵĽ»µć£©B”¢P£®
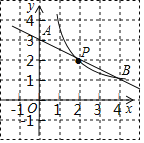
£Ø1£©Ē󷓱ȥżŗÆŹżŗĶŅ»“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©¹Ū²ģĶ¼Ļó£¬Ö±½ÓŠ“³öŅ»“ĪŗÆŹżÖµ“óÓŚ·“±ČĄżŗÆŹżÖµŹ±xµÄȔֵ·¶Ī§ŹĒ£ŗ”” ””£®
£Ø3£©ŌŚĶ¼ÖŠÓĆÖ±³ßŗĶ2BĒ¦±Ź»³öĮ½øö¾ŲŠĪ£Ø²»Š“»·Ø£©£¬ŅŖĒóĆæøö¾ŲŠĪ¾łŠčĀś×ćĻĀĮŠĮ½øöĢõ¼ž£ŗ
¢ŁĖÄøö¶„µć¾łŌŚøńµćÉĻ£¬ĒŅĘäÖŠĮ½øö¶„µć·Ö±šŹĒµćO£¬µćP£»
¢Ś¾ŲŠĪµÄĆ껿µČÓŚkµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
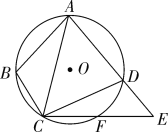
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() ŹĒ
ŹĒ![]() µÄĶā½ÓŌ²£¬Į¬½įOA”¢OB”¢OC£¬ŃÓ³¤BOÓėAC½»ÓŚµćD£¬Óė
µÄĶā½ÓŌ²£¬Į¬½įOA”¢OB”¢OC£¬ŃÓ³¤BOÓėAC½»ÓŚµćD£¬Óė![]() ½»ÓŚµćF£¬ŃÓ³¤BAµ½µćG£¬Ź¹µĆ
½»ÓŚµćF£¬ŃÓ³¤BAµ½µćG£¬Ź¹µĆ![]() £¬Į¬½ÓFG.
£¬Į¬½ÓFG.
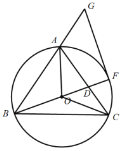
±øÓĆĶ¼
£Ø1£©ĒóÖ¤£ŗFGŹĒ![]() µÄĒŠĻߣ»
µÄĒŠĻߣ»
£Ø2£©Čō![]() µÄ°ė¾¶ĪŖ4.
µÄ°ė¾¶ĪŖ4.
¢Łµ±![]() £¬ĒóADµÄ³¤¶Č£»
£¬ĒóADµÄ³¤¶Č£»
¢Śµ±![]() ŹĒÖ±½ĒČż½ĒŠĪŹ±£¬Ēó
ŹĒÖ±½ĒČż½ĒŠĪŹ±£¬Ēó![]() µÄĆ껿.
µÄĆ껿.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
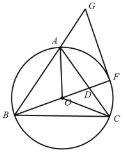
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ACEÖŠ£¬AC£½CE£¬”ŃO¾¹żµćA£¬C£¬ĒŅÓė±ßAE£¬CE·Ö±š½»ÓŚµćD£¬F£¬µćBŹĒĮÓ»”ACÉĻµÄŅ»µć£¬ĒŅ![]() £¬Į¬½ÓAB£¬BC£¬CD.
£¬Į¬½ÓAB£¬BC£¬CD.
(1)ĒóÖ¤£ŗ”÷CDE”Õ”÷ABC£»
(2)ĢīæÕ£ŗČōACĪŖ”ŃOµÄÖ±¾¶£¬Ōņµ±”÷ACEµÄŠĪדĪŖ Ź±£¬ĖıߊĪABCDĪŖÕż·½ŠĪ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ“óĀ„ABÕżĒ°·½ÓŠŅ»Š±ĘĀCD£¬ĘĀ½Ē”ĻDCE=30”ć£¬Ā„øßAB=60Ć×£¬ŌŚŠ±ĘĀĻĀµÄµćC“¦²āµĆĀ„¶„BµÄŃö½ĒĪŖ60”ć£¬ŌŚŠ±ĘĀÉĻµÄD“¦²āµĆĀ„¶„BµÄŃö½ĒĪŖ45”ć£¬ĘäÖŠµćA,C,EŌŚĶ¬Ņ»Ö±ĻßÉĻ.
£Ø1£©ĒóĘĀµ×Cµćµ½“óĀ„¾ąĄėACµÄÖµ£»
£Ø2£©ĒóŠ±ĘĀCDµÄ³¤¶Č.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”涫¶«Ķę¾ßÉĢµźÓĆ500ŌŖ¹ŗ½ųŅ»ÅśÓĘÓĘĒņ£¬ŗÜŹÜÖŠŠ”ѧɜ»¶Ó£¬ÓĘÓĘĒņŗÜæģŹŪĶź£¬½Ó×ÅÓÖÓĆ900ŌŖ¹ŗ½ųµŚ¶žÅśÕāÖÖÓĘÓĘĒņ£¬Ėł¹ŗŹżĮæŹĒµŚŅ»ÅśŹżĮæµÄ1.5±¶£¬µ«ĆæĢ×½ų¼Ū¶ąĮĖ5ŌŖ£®
£Ø1£©ĒóµŚŅ»ÅśÓĘÓĘĒņĆæĢ׵Ľų¼ŪŹĒ¶ąÉŁŌŖ£»
£Ø2£©Čē¹ūÕāĮ½ÅśÓĘÓĘĒņĆæĢ׏Ū¼ŪĻąĶ¬£¬ĒŅČ«²æŹŪĶźŗó×ÜĄūČó²»µĶÓŚ25%£¬ÄĒĆ“ĆæĢ×ÓĘÓĘĒņµÄŹŪ¼ŪÖĮÉŁŹĒ¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ¶ž“ĪŗÆŹż![]() µÄĶ¼Ļó¹ż
µÄĶ¼Ļó¹ż![]() Į½µć£®
Į½µć£®
£Ø1£©Ēó“Ė¶ž“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©É趞“ĪŗÆŹżµÄĶ¼ĻóÓė![]() ÖįµÄĮķŅ»øö½»µćĪŖ
ÖįµÄĮķŅ»øö½»µćĪŖ![]() £¬Ēóµć
£¬Ēóµć![]() µÄ×ų±ź£»
µÄ×ų±ź£»
£Ø3£©ŌŚĶ¬Ņ»×ų±źĻµÖŠ»³ö“Ė¶ž“ĪŗÆŹż¼°Ö±Ļß![]() £¬²¢Š“³öµ±
£¬²¢Š“³öµ±![]() ŌŚŹ²Ć“·¶Ī§ÄŚŹ±£¬Ņ»“ĪŗÆŹżµÄÖµ“óÓŚ¶ž“ĪŗÆŹżµÄÖµ£®
ŌŚŹ²Ć“·¶Ī§ÄŚŹ±£¬Ņ»“ĪŗÆŹżµÄÖµ“óÓŚ¶ž“ĪŗÆŹżµÄÖµ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĻĀĶ¼1£¬½«Čż½Ē°å·ÅŌŚÕż·½ŠĪ![]() ÉĻ£¬Ź¹Čż½Ē°åµÄÖ±½Ē¶„µć
ÉĻ£¬Ź¹Čż½Ē°åµÄÖ±½Ē¶„µć![]() ÓėÕż·½ŠĪ
ÓėÕż·½ŠĪ![]() µÄ¶„µć
µÄ¶„µć![]() ÖŲŗĻ£¬Čż½Ē°åµÄŅ»±ß½»
ÖŲŗĻ£¬Čż½Ē°åµÄŅ»±ß½»![]() ÓŚµć
ÓŚµć![]() £®ĮķŅ»±ß½»
£®ĮķŅ»±ß½»![]() µÄŃÓ³¤ĻßÓŚµć
µÄŃÓ³¤ĻßÓŚµć![]() £®
£®
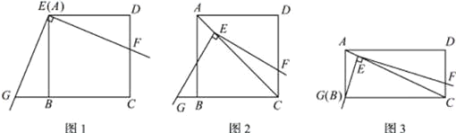
£Ø1£©¹Ū²ģ²ĀĻė£ŗĻ߶Ī![]() ÓėĻ߶Ī
ÓėĻ߶Ī![]() µÄŹżĮæ¹ŲĻµŹĒ £»
µÄŹżĮæ¹ŲĻµŹĒ £»
£Ø2£©Ģ½¾æÖ¤Ć÷£ŗČēĶ¼2£¬ŅʶÆČż½Ē°å£¬Ź¹¶„µć![]() Ź¼ÖÕŌŚÕż·½ŠĪ
Ź¼ÖÕŌŚÕż·½ŠĪ![]() µÄ¶Ō½ĒĻß
µÄ¶Ō½ĒĻß![]() ÉĻ£¬ĘäĖūĢõ¼ž²»±ä£¬£Ø1£©ÖŠµÄ½įĀŪŹĒ·ńČŌČ»³ÉĮ¢£æČō³ÉĮ¢£¬ĒėøųÓčÖ¤Ć÷£ŗČō²»³ÉĮ¢£®ĒėĖµĆ÷ĄķÓÉ£ŗ
ÉĻ£¬ĘäĖūĢõ¼ž²»±ä£¬£Ø1£©ÖŠµÄ½įĀŪŹĒ·ńČŌČ»³ÉĮ¢£æČō³ÉĮ¢£¬ĒėøųÓčÖ¤Ć÷£ŗČō²»³ÉĮ¢£®ĒėĖµĆ÷ĄķÓÉ£ŗ
£Ø3£©ĶŲÕ¹ŃÓÉģ£ŗČēĶ¼3£¬½«£Ø2£©ÖŠµÄ”°Õż·½ŠĪ![]() ”±øÄĪŖ”°¾ŲŠĪ
”±øÄĪŖ”°¾ŲŠĪ![]() ”±£¬ĒŅŹ¹Čż½Ē°åµÄŅ»±ß¾¹żµć
”±£¬ĒŅŹ¹Čż½Ē°åµÄŅ»±ß¾¹żµć![]() £¬ĘäĖūĢõ¼ž²»±ä£¬Čō
£¬ĘäĖūĢõ¼ž²»±ä£¬Čō![]() ”¢
”¢![]() £¬Ēó
£¬Ēó![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com