练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
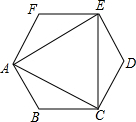
    6．顺次连接正六边形的三个不相邻的顶点，得到如图的图形，下列说法错误的是（　　）
    A．△ACE是等边三角形B．既是轴对称图形也是中心对称图形
    C．连接AD，则AD分别平分∠EAC与∠EDCD．图中一共能画出3条对称轴

    分析 根据正多边形的性质和轴对称图形与中心对称图形的定义解答．

    解答 解：A、∵多边形ABCDEF是正六边形，
    ∴△ACE是等边三角形，故本选项正确；
    B、∵△ACE是等边三角形，∴是轴对称图形，不是中心对称图形，故本选项错误；
    C、∵△ACE是等边三角形，∴连接AD，则AD分别平分∠EAC与∠EDC，故本选项正确；
    D、∵△ACE是等边三角形，∴图中一共能画3条对称轴，故本选项正确．
    故选B．

    点评 本题考查的是正多边形和圆，熟知正多边形与等边三角形的性质是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    16．某通讯公司推出了A、B两种不同上网计费方式如下表：
    项目
    项目/计费方式月租费（元）限流量（MB）超流量（元/MB）
    A5300.5
    B10701
    设一个月内移动电话的流量为tMB（t≥0），根据要求回答下列问题．
    （1）用含t的式子填写下表：
    流量/计费方式t≥3030≤t≤70t＞70
    A种计费（元）50.5t-10 0.5t-10 
    B种计费（元）1010t-60 
    （2）当t为何值时，两种计费方式的费用相等；
    （3）当50＜t＜100时，你认为选择哪种计费方式更省钱，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．我市为了鼓励居民节约用水，对居民生活用水的收费实行阶梯式计量水价的方法，具体规定如下：
     各阶梯 月用水量 基本水价（元、立方米）
     第一阶梯 不超过28立方米的部分 2
     第二阶梯 超过28立方米且不超过40立方米的部分 2.5
     第三阶梯 超过40立方米的部分 3
    设某户每月用水量为x立方米，应收水费y元
    （1）分别写出每月用水量在三个不同阶梯时，y与x的函数关系式．
    （2）已知小明家4月份缴纳水费83元，则他家该月共用水多少立方米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．设a，b，c是△ABC的三边长，二次函数y=（a-$\frac{b}{2}$）x2-cx-a-$\frac{b}{2}$在x=1时取最小值-$\frac{8}{5}$b，则sinA=$\frac{4}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

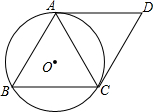    1．如图，⊙O是△ABC的外接圆，分别过A、C两点作⊙O的两条切线AD、CD，它们的交点为D，且AD∥BC，CD∥AB．
    （1）试说明四边形ABCD是菱形；
    （2）若⊙O的半径是2$\sqrt{3}$，求四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

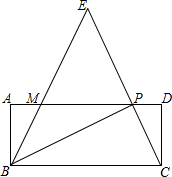    11．如图，矩形ABCD中，P是边AD上的一动点，连接BP、CP，过点B作射线交线段CP的延长线于点E，交AD边于点M，且使得∠ABE=∠CBP，
    如果AB=2，BC=5，AP=x，PM=y．
    （1）说明△ABM∽△APB；并求出y关于x的函数关系式，写出自变量x的取值范围；
    （2）当AP=4时，求sin∠EBP的值；
    （3）如果△EBC是以∠EBC为底角的等腰三角形，求AP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图1，点E，F分别在正方形ABCD的边BC，CD上，∠EAF=45°，连接EF．延长CD至G，使GD=EB，连接AG，易证△AFG≌△AFE．所以EF，BE，DF之间的数量关系为 EF=DF+BE．
    （1）如图2，点E，F分别在正方形ABCD的边BC，CD的延长线上，∠EAF=45°，连接EF．试猜想EF，BE，DF之间的数量关系；（直接写出结果，不需证明）
    （2）如图3，点E，F分别在正方形ABCD的边CB，DC的延长线上，∠EAF=45°，连接EF．试猜想EF，BE，DF之间的数量关系，并加以证明；
    （3）如图4，点E，F在正方形ABCD的对角线BD上，∠EAF=45°，若BE=2，DF=1，请直接写出EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

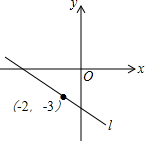    15．如图的坐标平面上，有一条通过点（-2，-3）的直线l．若四点（-2，a）、（0，b）、（c，0）、（d，-1）在l上，则下列数值判断正确是（　　）
    A．a=2B．b＞-3C．c＜-2D．d=3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

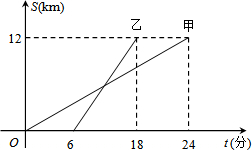    16．如图，表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动．甲、乙两人前往目的地所行驶的路程S（千米）随时间t（分）变化的函数图象，则每分钟乙比甲多行驶的路程是（　　）
    A．0.5千米B．1千米C．1.5千米D．2千米

    查看答案和解析>>

    同步练习册答案