
ЁОЬтФПЁПдФЖСВФСЯЃКЧѓНтвЛдЊвЛДЮЗНГЬЃЌашвЊИљОнЕШЪНЕФЛљБОаджЪЃЌАбЗНГЬзЊЛЏЮЊxЃНaЕФаЮЪНЃЛЧѓНтЖўдЊвЛДЮЗНГЬзщЃЌашвЊЭЈЙ§ЯћдЊАбЫќзЊЛЏЮЊвЛдЊвЛДЮЗНГЬРДНтЃЛЧѓНтШ§дЊвЛДЮЗНГЬзщЃЌашвЊАбЫќзЊЛЏЮЊЖўдЊвЛДЮЗНГЬзщРДНтЃЛЧѓНтвЛдЊЖўДЮЗНГЬЃЌашвЊАбЫќзЊЛЏЮЊСНИівЛдЊвЛДЮЗНГЬРДНтЃЛЧѓНтЗжЪНЗНГЬЃЌашвЊЭЈЙ§ШЅЗжФИАбЫќзЊЛЏЮЊећЪНЗНГЬРДНтЃЌИїРрЗНГЬЕФНтЗЈВЛОЁЯрЭЌЃЌЕЋЪЧЫќУЧЖМгУЕНвЛжжЙВЭЌЕФЛљБОЪ§бЇЫМЯыЉзЊЛЏЃЌМДАбЮДжЊзЊЛЏЮЊвбжЊРДЧѓНтЃЎ
гУЁАзЊЛЏЁАЕФЪ§бЇЫМЯыЃЌЮвУЧЛЙПЩвдНтвЛаЉаТЕФЗНГЬЃЎ
Р§ШчЃЌНтвЛдЊШ§ДЮЗНГЬx3+x2Љ2xЃН0ЃЌЭЈЙ§вђЪНЗжНтАбЫќзЊЛЏЮЊxЃЈx2+xЉ2ЃЉЃН0ЃЌЭЈЙ§НтЗНГЬxЃН0КЭx2+xЉ2ЃН0ЃЌПЩЕУдЗНГЬx3+x2Љ2xЃН0ЕФНтЃЎ
дйР§ШчЃЌНтИљКХЯТКЌгаРДжЊЪ§ЕФЗНГЬЃК![]() ЃНxЃЌЭЈЙ§СНБпЭЌЪБЦНЗНАбЫќзЊЛЏЮЊ2x+3ЃНx2ЃЌНтЕУЃКx1ЃН3ЃЌx2ЃНЉ1ЃЎвђЮЊ2x+3Ён0ЃЌЧвxЁн0ЃЌЫљвдxЃНЉ1ВЛЪЧдЗНГЬЕФИљЃЌxЃН3ЪЧдЗНГЬЕФНтЃЎ
ЃНxЃЌЭЈЙ§СНБпЭЌЪБЦНЗНАбЫќзЊЛЏЮЊ2x+3ЃНx2ЃЌНтЕУЃКx1ЃН3ЃЌx2ЃНЉ1ЃЎвђЮЊ2x+3Ён0ЃЌЧвxЁн0ЃЌЫљвдxЃНЉ1ВЛЪЧдЗНГЬЕФИљЃЌxЃН3ЪЧдЗНГЬЕФНтЃЎ
ЃЈ1ЃЉЮЪЬтЃКЗНГЬx3+x2Љ2xЃН0ЕФНтЪЧx1ЃН0ЃЌx2ЃНЁЁ ЁЁЃЌx3ЃНЁЁ ЁЁЃЎ
ЃЈ2ЃЉЭиеЙЃКЧѓЗНГЬ![]() ЃНxЉ1ЕФНтЃЛ
ЃНxЉ1ЕФНтЃЛ
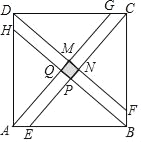
ЃЈ3ЃЉгІгУЃКдквЛИіБпГЄЮЊ1ЕФе§ЗНаЮжаЙЙдьвЛИіШчЭМЫљЪОЕФе§ЗНаЮЃЛдке§ЗНаЮABCDБпЩЯвРДЮНиШЁAEЃНBFЃНCGЃНDHЃН![]() ЃЌСЌНгAGЃЌBHЃЌCEЃЌDFЃЌЕУЕНе§ЗНаЮMNPQЃЌШєаЁе§ЗНаЮMNPQЃЈЭМжавѕгАВПЗжЃЉЕФБпГЄЮЊ
ЃЌСЌНгAGЃЌBHЃЌCEЃЌDFЃЌЕУЕНе§ЗНаЮMNPQЃЌШєаЁе§ЗНаЮMNPQЃЈЭМжавѕгАВПЗжЃЉЕФБпГЄЮЊ![]() ЃЌЧѓnЕФжЕЃЎ
ЃЌЧѓnЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ1ЃЌЉ2ЃЛЃЈ2ЃЉЯъМћНтЮіЃЛЃЈ3ЃЉnЕФжЕЮЊ9ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУвђЪНЗжНтЗЈЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉЯШЗНГЬСНБпЦНЗНзЊЛЏГЩећЪНЗНГЬЃЌдйЧѓвЛдЊЖўДЮЗНГЬЕФНтЃЌзюКѓБиаыМьбщЃЛ
ЃЈ3ЃЉЯШИљОнЙДЙЩЖЈРэЧѓГіAGЃЌНјЖјЕУГіsinЁЯAGDЃН ЃЌдйЙЙдьГіжБНЧШ§НЧаЮЃЌЕУГіsinЁЯEAWЃН
ЃЌдйЙЙдьГіжБНЧШ§НЧаЮЃЌЕУГіsinЁЯEAWЃН![]() ЃЌНјЖјНЈСЂЗНГЬЃЌРћгУЃЈ2ЃЉЕФЗНЗЈНтДЫЗНГЬМДПЩЕУГіНсТлЃЎ
ЃЌНјЖјНЈСЂЗНГЬЃЌРћгУЃЈ2ЃЉЕФЗНЗЈНтДЫЗНГЬМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉЁпx3+x2Љ2xЃН0ЃЌ
ЁрxЃЈxЉ1ЃЉЃЈx+2ЃЉЃН0
ЁрxЃН0ЛђxЉ1ЃН0Лђx+2ЃН0ЃЌ
Ёрx1ЃН0ЃЌx2ЃН1ЃЌx3ЃНЉ2ЃЌ
ЙЪД№АИЮЊ1ЃЌЉ2ЃЛ
ЃЈ2ЃЉИјЗНГЬ
![]() ЃНxЉ1ЕФСНБпЦНЗНЕУЃЌ3x2Љ3xЉ2ЃНЃЈxЉ1ЃЉ2ЃЌ
ЃНxЉ1ЕФСНБпЦНЗНЕУЃЌ3x2Љ3xЉ2ЃНЃЈxЉ1ЃЉ2ЃЌ
ЁрxЃН![]() ЛђxЃНЉ1ЃЌ
ЛђxЃНЉ1ЃЌ
Ёп3x2Љ3xЉ2Ён0ЧвxЉ1Ён0ЃЌ
ЁрxЃНЉ1ВЛЪЧдЗНГЬЕФНтЃЌxЃН![]() ЪЧдЗНГЬЕФНтЃЛ
ЪЧдЗНГЬЕФНтЃЛ
ЃЈ3ЃЉШчЭМЃЌ
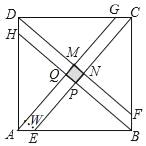
ЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
ЁрЁЯADCЃН90ЁуЃЌ
CDЁЮABЃЌ
ЁрЁЯAGDЃНЁЯGABЃЌ
ЁпCGЁЮAEЃЌCGЃНAEЃЌ
ЁрЫФБпаЮAECGЪЧЦНааЫФБпаЮЃЌ
ЁрAGЁЮECЃЌЕуEзїEWЁЮPQНЛAQгкWЃЌ
ЁрЫФБпаЮPQWEЪЧЦНааЫФБпаЮЃЌ
ЁрEWЃНPQЃН![]() ЃЌ
ЃЌ
ЁпЫФБпаЮMNPQЪЧе§ЗНаЮЃЌ
ЁрЁЯPQAЃН90ЁуЃЌ
ЁрЁЯAWEЃН90ЁуЃЌ
дкRtЁїADGжаЃЌADЃН1ЃЌDGЃН1Љ![]() ЃЌ
ЃЌ
ИљОнЙДЙЩЖЈРэЕУЃЌAGЃН![]()
![]() ЃЌ
ЃЌ
ЁрsinЁЯAGDЃН![]() ЃН
ЃН ЃЌ
ЃЌ
дкRtЁїAWDжаЃЌAEЃН![]() ЃЌEWЃН
ЃЌEWЃН![]() ЃЌ
ЃЌ
ЁрsinЁЯEAWЃН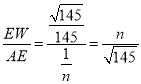 ЃЌ
ЃЌ
ЁпЁЯAGDЃНЁЯEAWЃЌ
Ёр ЃН
ЃН![]() ЃЌ
ЃЌ
СНБпЦНЗНЕУЃЌ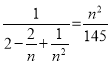 ЃЌ
ЃЌ
Ёр2n2Љ2n+1ЃН145ЃЌ
Ёрn2ЉnЉ72ЃН0ЃЌ
ЁрЃЈnЉ9ЃЉЃЈn+8ЃЉЃН0ЃЌ
ЁрnЃН9ЛђnЃНЉ8ЃЈгЩгкnЃО0ЃЌвђДЫЩсШЅЃЉЃЌ
ЁрnЃН9ЃЌ
МДЃКnЕФжЕЮЊ9ЃЎ


 ПЊаФПьРжМйЦкзївЕЪюМйзївЕЮїАВГіАцЩчЯЕСаД№АИ
ПЊаФПьРжМйЦкзївЕЪюМйзївЕЮїАВГіАцЩчЯЕСаД№АИ УћЬтбЕСЗЯЕСаД№АИ
УћЬтбЕСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() БпЩЯЕФИпЃЌЙ§Еу
БпЩЯЕФИпЃЌЙ§Еу![]() зї
зї![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЃЌ
ЃЌ![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЃЌ
ЃЌ![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЎ
ЃЎ
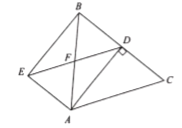
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮ![]() ЪЧОиаЮЃЛ
ЪЧОиаЮЃЛ
ЃЈ2ЃЉЧѓЫФБпаЮ![]() ЕФжмГЄЃЎ
ЕФжмГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуEЪЧЫФБпаЮABCDЕФЖдНЧЯпЃТЃФЩЯвЛЕуЃЌЧвЁЯBACЃНЁЯBDCЃНЁЯDAE.
ЂйЪдЫЕУїBEЁЄADЃНCDЁЄAEЃЛ
ЂкИљОнЭМаЮЬиЕуЃЌВТЯы![]() ПЩФмЕШгкФФСНЬѕЯпЖЮЕФБШ?ВЂжЄУїФуЕФВТЯыЃЌЃЈжЛаыаДГігаЯпЖЮЕФвЛзщМДПЩЃЉ
ПЩФмЕШгкФФСНЬѕЯпЖЮЕФБШ?ВЂжЄУїФуЕФВТЯыЃЌЃЈжЛаыаДГігаЯпЖЮЕФвЛзщМДПЩЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃзщжЏбЇЩњВЮМгЁААВШЋжЊЪЖОКШќЁБЃЈТњЗжЮЊ![]() ЗжЃЉЃЌВтЪдНсЪјКѓЃЌеХРЯЪІДгЦпФъМЖ
ЗжЃЉЃЌВтЪдНсЪјКѓЃЌеХРЯЪІДгЦпФъМЖ![]() УћбЇЩњжаЫцЛњЕиГщШЁВПЗжбЇЩњЕФГЩМЈЛцжЦСЫЬѕаЮЭГМЦЭМЃЌШчЭМ
УћбЇЩњжаЫцЛњЕиГщШЁВПЗжбЇЩњЕФГЩМЈЛцжЦСЫЬѕаЮЭГМЦЭМЃЌШчЭМ![]() ЫљЪОЃЎЪдИљОнЭГМЦЭМЬсЙЉЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЫљЪОЃЎЪдИљОнЭГМЦЭМЬсЙЉЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
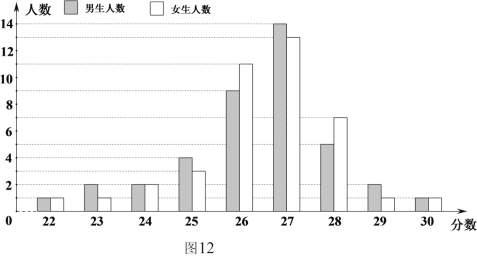
ЃЈ1ЃЉеХРЯЪІГщШЁЕФетВПЗжбЇЩњжаЃЌЙВга УћФаЩњЃЌ УћХЎЩњЃЛ
ЃЈ2ЃЉеХРЯЪІГщШЁЕФетВПЗжбЇЩњжаЃЌХЎЩњГЩМЈЕФжкЪ§ЪЧ ЃЛ
ЃЈ3ЃЉШєНЋВЛЕЭгк![]() ЗжЕФГЩМЈЖЈЮЊгХауЃЌЧыЙРМЦЦпФъМЖ
ЗжЕФГЩМЈЖЈЮЊгХауЃЌЧыЙРМЦЦпФъМЖ![]() УћбЇЩњжаГЩМЈЮЊгХауЕФбЇЩњШЫЪ§ДѓдМЪЧЖрЩй.
УћбЇЩњжаГЩМЈЮЊгХауЕФбЇЩњШЫЪ§ДѓдМЪЧЖрЩй.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊДњЪ§ЪН![]() ЃЈnЁйЃ2ЃЉЃЎ
ЃЈnЁйЃ2ЃЉЃЎ
ЃЈ1ЃЉЂйгУКЌnЕФДњЪ§ЪНБэЪОmЃЛ
ЂкШєmЁЂnОљШЁећЪ§ЃЌЧѓmЁЂnЕФжЕЃЎ
ЃЈ2ЃЉЕБnШЁaЁЂbЪБЃЌmЖдгІЕФжЕЮЊcЁЂdЃЎ ЕБЃ2ЃМbЃМaЪБЃЌЪдБШНЯcЁЂdЕФДѓаЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЫЎЙћОЯњЩЬЩЯдТЗнЯњЪлвЛжжаТЩЯЪаЕФЫЎЙћЃЌЦНОљЪлМлЮЊ10дЊ/ЧЇПЫЃЌдТЯњЪлСПЮЊ1000ЧЇПЫ.ОЪаГЁЕїВщЃЌШєНЋИУжжЫЎЙћМлИёЕїЕЭжСxдЊ/ЧЇПЫЃЌдђБОдТЗнЯњЪлСПyЃЈЧЇПЫЃЉгыxЃЈдЊ/ЧЇПЫЃЉжЎМфЗћКЯвЛДЮКЏЪ§ЙиЯЕЃЌВЂЧвЕУЕНСЫБэжаЕФЪ§ОнЃК
МлИёxЃЈдЊ/ЧЇПЫЃЉ | 7 | 5 |
МлИёyЃЈЧЇПЫЃЉ | 2000 | 4000 |
ЃЈ1ЃЉЧѓyгыxжЎМфЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉвбжЊИУжжЫЎЙћЩЯдТЗнЕФГЩБОМлЮЊ5дЊ/ЧЇПЫЃЌБОдТЗнЕФГЩБОМлЮЊ4дЊ/ЧЇПЫЃЌвЊЪЙБОдТЗнЯњЪлИУжжЫЎЙћЫљЛёРћШѓБШЩЯдТЗндіМг20ЃЅЃЌЭЌЪБгжвЊШУЙЫПЭЕУЕНЪЕЛнЃЌФЧУДИУжжЫЎЙћМлИёУПЧЇПЫгІЕїЕЭжСЖрЩйдЊ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌвЛДБТЅЗПABБГКѓгавЛЬЈНзCDЃЌЬЈНзУПВуИп0.2УзЃЌЧвAC=14.5УзЃЌNF=0.2УзЃЎЩшЬЋбєЙтЯпгыЫЎЦНЕиУцЕФМаНЧЮЊІСЃЌЕБІС=56.3ЁуЪБЃЌВтЕУТЅЗПдкЕиУцЩЯЕФгАГЄAE=10УзЃЌЯжгавЛжЛаЁУЈЫЏдкЬЈНзЕФNFетВуЩЯЩЙЬЋбєЃЎ
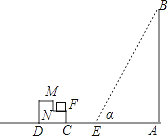
ЃЈ1ЃЉЧѓТЅЗПЕФИпЖШдМЮЊЖрЩйУзЃП
ЃЈ2ЃЉЙ§СЫвЛЛсЖљЃЌЕБІС=45ЁуЪБЃЌЮЪаЁУЈФмЗёЛЙЩЙЕНЬЋбєЃПЧыЫЕУїРэгЩЃЎЃЈВЮПМЪ§ОнЃКsin56.3ЁуЁж0.83ЃЌcos56.3ЁуЁж0.55ЃЌtan56.3ЁуЁж1.5ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛПщжБНЧШ§НЧаЮЕФжНЦЌЃЌСНжБНЧБпAC=6cmЃЌBC=8cmЃЌЯжНЋжБНЧБпACбижБЯпADелЕўЃЌЪЙЫќТфдкаББпABЩЯЃЌЧвгыAEжиКЯЃЌдђCDЕШгкЃЈЁЁЁЁ ЃЉ.

A. 2 cm B. 4 cm C. 3 cm D. 5 cm
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫЋЧњЯп![]() ЃЈxЃО0ЃЉЩЯгавЛЕуAЃЈ1ЃЌ5ЃЉЃЌЙ§ЕуAЕФжБЯпy=mx+nгыxжсНЛгкЕуCЃЈ6ЃЌ0ЃЉЃЎ
ЃЈxЃО0ЃЉЩЯгавЛЕуAЃЈ1ЃЌ5ЃЉЃЌЙ§ЕуAЕФжБЯпy=mx+nгыxжсНЛгкЕуCЃЈ6ЃЌ0ЃЉЃЎ
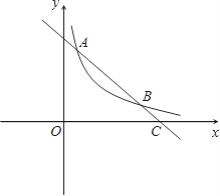
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉСЌНгOAЁЂOBЃЌЧѓЁїAOBЕФУцЛ§ЃЛ
ЃЈ3ЃЉИљОнЭМЯѓжБНгаДГідкЕквЛЯѓЯоФкЗДБШР§КЏЪ§жЕДѓгквЛДЮКЏЪ§жЕЪБxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com