

分析 (1)①在等腰直角三角形ACB中,由勾股定理先求得AB的长,然后根据PA的长,可求得PB的长;过点C作CD⊥AB,垂足为D,从而可求得CD、PD的长,然后在Rt三角形CDP中依据勾股定理可求得PC的长;②△ACB为等腰直角三角形,CD⊥AB,从而可求得:CD=AD=DB,然后根据AP=DC-PD,PB=DC+PD,可证明AP2+BP2=2PC2,因为在Rt△PCQ中,PQ2=2CP2,所以可得出AP2+BP2=PQ2的结论;
(2)过点C作CD⊥AB,垂足为D,则AP=(AD+PD)=(DC+PD),PB=(DP-BD)=(PD-DC),可证明AP2+BP2=2PC2,因为在Rt△PCQ中,PQ2=2CP2,所以可得出AP2+BP2=PQ2的结论;
(3)根据点P所在的位置画出图形,然后依据题目中的比值关系求得PD的长(用含有CD的式子表示),然后在Rt△ACP和Rt△DCP中由勾股定理求得AC和PC的长度即可.
解答 解:(1)如图①:
①∵△ABC是等腰直直角三角形,AC=1+$\sqrt{3}$
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{2A{C}^{2}}$=$\sqrt{2}$+$\sqrt{6}$,
∵PA=$\sqrt{2}$,
∴PB=$\sqrt{6}$,
∵△ABC和△PCQ均为等腰直角三角形,
∴AC=BC,PC=CQ,∠ACP=∠BCQ,
∴△APC≌△BQC.
∴BQ=AP=$\sqrt{2}$,∠CBQ=∠A=45°.
∴△PBQ为直角三角形.
∴PQ=$2\sqrt{2}$.
∴PC=$\frac{\sqrt{2}}{2}×$PQ=2.
故答案为:$\sqrt{6}$,2;
②如图1.
∵△ACB为等腰直角三角形,CD⊥AB,
∴CD=AD=DB.
∵AP2=(AD-PD)2=(DC-PD)2=DC2-2DC•PD+PD2,PB2=(DB+PD)2=(DC+DP)2=CD2+2DC•PD+PD2
∴AP2+BP2=2CD2+2PD2,
∵在Rt△PCD中,由勾股定理可知:PC2=DC2+PD2,
∴AP2+BP2=2PC2.
∵△CPQ为等腰直角三角形,
∴2PC2=PQ2.
∴AP2+BP2=PQ2
(2)如图②:过点C作CD⊥AB,垂足为D.
∵△ACB为等腰直角三角形,CD⊥AB,
∴CD=AD=DB.
∵AP2=(AD+PD)2=(DC+PD)2=CD2+2DC•PD+PD2,
PB2=(DP-BD)2=(PD-DC)2=DC2-2DC•PD+PD2,
∴AP2+BP2=2CD2+2PD2,
∵在Rt△PCD中,由勾股定理可知:PC2=DC2+PD2,
∴AP2+BP2=2PC2.
∵△CPQ为等腰直角三角形,
∴2PC2=PQ2.
∴AP2+BP2=PQ2.
(3)如图③:过点C作CD⊥AB,垂足为D.
①当点P位于点P1处时.
∵$\frac{{P}_{1}A}{{P}_{1}B}=\frac{1}{3}$,
∴${P}_{1}A=\frac{1}{4}AB=\frac{1}{2}DC$.
∴${P}_{1}D=\frac{1}{2}DC$.
在Rt△CP1D中,由勾股定理得:$C{P}_{1}=\sqrt{D{C}^{2}+{P}_{1}{D}^{2}}$=$\sqrt{D{C}^{2}+(\frac{1}{2}DC)^{2}}$=$\frac{\sqrt{5}}{2}$DC,
在Rt△ACD中,由勾股定理得:AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=$\sqrt{2D{C}^{2}}$=$\sqrt{2}$DC,
∴$\frac{{P}_{1}C}{AC}=\frac{\frac{\sqrt{5}}{2}DC}{\sqrt{2}DC}=\frac{\sqrt{10}}{4}$.
②当点P位于点P2处时.
∵$\frac{{P}_{2}A}{{P}_{2}B}$=$\frac{1}{3}$,
∴${P}_{2}A=\frac{1}{2}AB=CD$.
在Rt△CP2D中,由勾股定理得:${P}_{2}C=\sqrt{D{C}^{2}+{P}_{2}{D}^{2}}$=$\sqrt{D{C}^{2}+(2DC)^{2}}$=$\sqrt{5}DC$,
在Rt△ACD中,由勾股定理得:AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=$\sqrt{2D{C}^{2}}$=$\sqrt{2}$DC,
∴$\frac{{P}_{2}C}{AC}=\frac{\sqrt{5}DC}{\sqrt{2}DC}=\frac{\sqrt{10}}{2}$.
综上所述,$\frac{PC}{AC}$的比值为$\frac{\sqrt{10}}{4}$或$\frac{\sqrt{10}}{2}$.
点评 本题主要考查的是等腰直角三角形的性质和勾股定理的应用,根据等腰直角三角形的性质证得:CD=AD=DB,将PA、PA、PQ、AC、PC用含DC的式子表示出来是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | x1+y1=x2+y2 | B. | x1y2=x2y1 | C. | $\frac{{x}_{1}}{{x}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$ | D. | $\frac{{x}_{2}}{{x}_{1}}$=$\frac{{y}_{1}}{{y}_{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某冷饮点一天售出各种口味雪糕数量的扇形统计图如图所示,其中售出红豆口味的雪糕200支.
某冷饮点一天售出各种口味雪糕数量的扇形统计图如图所示,其中售出红豆口味的雪糕200支.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
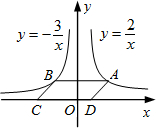 如图,点A是反比例函数y=$\frac{2}{x}$(x>0)的图象上任意一点,AB∥x轴并反比例函数y=-$\frac{3}{x}$的图象于点B,以AB为边作?ABCD,其中点C,D在x轴上,则?ABCD的面积为( )
如图,点A是反比例函数y=$\frac{2}{x}$(x>0)的图象上任意一点,AB∥x轴并反比例函数y=-$\frac{3}{x}$的图象于点B,以AB为边作?ABCD,其中点C,D在x轴上,则?ABCD的面积为( )| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
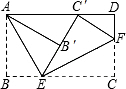 将矩形ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=$\sqrt{3}$,折叠后,点C落在AD边上的C′处,并且点B落在EC′边上的B′处,则BC的长为( )
将矩形ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=$\sqrt{3}$,折叠后,点C落在AD边上的C′处,并且点B落在EC′边上的B′处,则BC的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
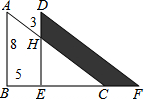 如图,原来是重叠的两个直角三角形,将其中一个三角形沿着BC方向平移线段BE的距离,就得到此图形,下列结论正确的有( )
如图,原来是重叠的两个直角三角形,将其中一个三角形沿着BC方向平移线段BE的距离,就得到此图形,下列结论正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com