
 ×īŠ”ÖµĪŖ-4£¬
×īŠ”ÖµĪŖ-4£¬| -1+3 |
| 2 |
| 32+32 |
| 2 |
|
| 21 |
| 4 |
| -3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 21 |
| 4 |
| 15 |
| 4 |
| 3 |
| 2 |
| 15 |
| 4 |
| 21 |
| 4 |
| ||
| 2 |
9
| ||
| 8 |
| 1 |
| 2 |
| 2 |
9
| ||
| 8 |
| 27 |
| 8 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ČēĶ¼£¬¶ž“ĪŗÆŹżµÄĶ¼Ļó¾¹żµćD£Ø0£¬
ČēĶ¼£¬¶ž“ĪŗÆŹżµÄĶ¼Ļó¾¹żµćD£Ø0£¬| 7 |
| 9 |
| 3 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
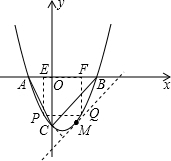
 ČēĶ¼£¬¶ž“ĪŗÆŹży=ax2+bx+cµÄĶ¼ĻóÓėxÖį½»ÓŚB”¢CĮ½µć£¬ÓėyÖį½»ÓŚµćA£Ø0£¬-3£©£¬”ĻABC=45”ć£¬”ĻACB=60”ć£¬ĒóÕāøö¶ž“ĪŗÆŹż½āĪöŹ½£®
ČēĶ¼£¬¶ž“ĪŗÆŹży=ax2+bx+cµÄĶ¼ĻóÓėxÖį½»ÓŚB”¢CĮ½µć£¬ÓėyÖį½»ÓŚµćA£Ø0£¬-3£©£¬”ĻABC=45”ć£¬”ĻACB=60”ć£¬ĒóÕāøö¶ž“ĪŗÆŹż½āĪöŹ½£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ij¹«Ė¾ĶĘ³öĮĖŅ»ÖÖøߊ§»·±£ŠĶĻ“µÓÓĆĘ·£¬Äź³õÉĻŹŠŗ󣬹«Ė¾¾ĄśĮĖ“Óæ÷Ėšµ½ÓÆĄūµÄ¹ż³Ģ£¬ČēĶ¼µÄ¶ž“ĪŗÆŹżĶ¼Ļó£Ø²æ·Ö£©æĢ»ĮĖøĆ¹«Ė¾Äź³õŅŌĄ“ĄŪ»żĄūČós£ØĶņŌŖ£©ÓėŹ±¼ät£ØŌĀ£©Ö®¼äµÄ¹ŲĻµ£Ø¼“Ē°tøöŌĀµÄĄūČó×ÜŗĶsÓėtÖ®¼äµÄ¹ŲĻµ£©£®øł¾ŻĶ¼ĻóĢį¹©µÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
ij¹«Ė¾ĶĘ³öĮĖŅ»ÖÖøߊ§»·±£ŠĶĻ“µÓÓĆĘ·£¬Äź³õÉĻŹŠŗ󣬹«Ė¾¾ĄśĮĖ“Óæ÷Ėšµ½ÓÆĄūµÄ¹ż³Ģ£¬ČēĶ¼µÄ¶ž“ĪŗÆŹżĶ¼Ļó£Ø²æ·Ö£©æĢ»ĮĖøĆ¹«Ė¾Äź³õŅŌĄ“ĄŪ»żĄūČós£ØĶņŌŖ£©ÓėŹ±¼ät£ØŌĀ£©Ö®¼äµÄ¹ŲĻµ£Ø¼“Ē°tøöŌĀµÄĄūČó×ÜŗĶsÓėtÖ®¼äµÄ¹ŲĻµ£©£®øł¾ŻĶ¼ĻóĢį¹©µÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
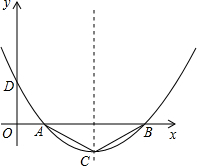
 ČēĶ¼£¬¶ž“ĪŗÆŹży=ax2+bx+cµÄĶ¼ĻóÓėxÖįĻą½»ÓŚĮ½øöµć£¬øł¾ŻĶ¼Ļó»Ų“š£ŗ£Ø1£©b
ČēĶ¼£¬¶ž“ĪŗÆŹży=ax2+bx+cµÄĶ¼ĻóÓėxÖįĻą½»ÓŚĮ½øöµć£¬øł¾ŻĶ¼Ļó»Ų“š£ŗ£Ø1£©b²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com