
【题目】如图,矩形ABCD中,AD=10,AB=8,点E为边DC上一动点,连接AE,把△ADE沿AE折叠,使点D落在点D′处,当△DD′C是直角三角形时,DE的长为_____.
【答案】4或5.
【解析】

∵△ADE沿AE折叠,使点D落在点D′处,
∴DE=D′E,AD=AD′=10,
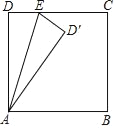
(1)当∠DD′C=90°时,如图1,
∵DE=D′E,
∴∠1=∠2,
∵∠1+∠4=90°,∠2+∠3=90°,
∴∠3=∠4,
∴ED′=EC,
∴DE=EC=![]() CD=4;
CD=4;
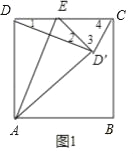
(2)当∠DCD′=90°时,则点D′落在BC上,如图2,
设DE=x,则ED′=x,CE=8﹣x,
∵AD′=AD=10,
∴在Rt△ABD′中,BD′=![]() =6,
=6,
∴CD′=4,
在Rt△CED′中,(8﹣x)2+42=x2,解得x=5,
即DE的长为5,
综上所述,当△DD′C是直角三角形时,DE的长为4或5.
故答案为4或5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,∠A=∠ABC=∠BCD=∠D=90°,AB=CD=5,AD=BC=13,点E为射线AD上的一个动点,若△ABE与△A'BE关于直线BE对称,当△A'BC为直角三角形时,AE的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中,BF、CF是角平分线,DE∥BC,分别交AB、AC于点D、E,DE经过点F.结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE; ③△ADE的周长=AB+AC;④BF=CF.其中正确的是______.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘救生船在码头A接到小岛C处一艘渔船的求救信号,立即出发,沿北偏东67°方向航行10海里到达小岛C处,将人员撤离到位于码头A正东方向的码头B,测得小岛C位于码头B的北偏西53°方向,求码头A与码头B的距离.【参考数据:sin23°≈0.39,cos23°≈0.92,tan23°≈0.42,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75】

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ ABC中,AB=AC,∠ BAC=90°,直角∠ EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF;②△ EPF是等腰直角三角形; ③2S四边形AEPF=S△ ABC; ④BE+CF=EF.当∠ EPF在△ ABC内绕顶点P旋转时(点E与A、B重合).上述结论中始终正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明学习电学知识后,用四个开关按键(每个开关按键闭合的可能性相等)、一个电源和一个灯泡设计了一个电路图
(1)若小明设计的电路图如图1(四个开关按键都处于打开状态)如图所示,求任意闭合一个开关按键,灯泡能发光的概率;

(2)若小明设计的电路图如图2(四个开关按键都处于打开状态)如图所示,求同时时闭合其中的两个开关按键,灯泡能发光的概率.(用列表或树状图法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案并简述购货方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com