
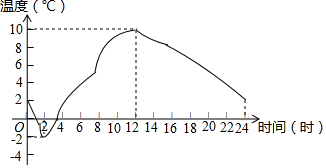
 如图是某地区春季某天的气温随时间的变化图象.请根据图象回答:
如图是某地区春季某天的气温随时间的变化图象.请根据图象回答:分析 (1)根据观察函数图象的纵坐标,可得最低气温,根据观察函数图象的横坐标,可得最低气温的时间;
(2)根据观察函数图象的纵坐标,可得最高气温,根据有理数的减法,可得温差;
(3)根据题意列出相应的算式,计算得到最高气温与最低气温,即可得到温差.
解答 解:(1)由图象可知2时气温最低,为-2℃.
(2)最高气温为10℃,最大温差为10-(-2)=10+2=12(℃).
(3)第二天该地区的最高气温不会高于10-10=0(℃),
最低气温不会低于-2-12=-2+(-12)=-14(℃);
最小温差是(10-12)-(-2-10)=-2-(-12)=10(℃).
点评 本题考查了函数图象、有理数的减法法则的应用,弄清题意、仔细观察函数图象的纵坐标得出气温,横坐标得出相应的时间是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
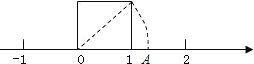 如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )| A. | 整数 | B. | 有理数 | C. | 分数 | D. | 无理数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com