
 ��ͼ�����ı���ABCD�У�AD��BC��AD=12cm��CD=8cm��BC=BD=20cm����P��B������BD���������˶����ٶ�Ϊ2cm/s��ͬʱ���߶�EF��DC������DA���������˶����ٶ�Ϊ2cm/s����BD��Q������PE�������˶�ʱ��Ϊt��s����0��t��5��������������⣺
��ͼ�����ı���ABCD�У�AD��BC��AD=12cm��CD=8cm��BC=BD=20cm����P��B������BD���������˶����ٶ�Ϊ2cm/s��ͬʱ���߶�EF��DC������DA���������˶����ٶ�Ϊ2cm/s����BD��Q������PE�������˶�ʱ��Ϊt��s����0��t��5��������������⣺���� ��1����PE��ABʱ���� $\frac{DE}{DA}$=$\frac{DP}{DB}$���г����̼��ɽ�����⣮
��2���á�PDE�ա�FBP������S�����PFCDE=S��PDE+S�ı���PFCD=S��FBP+S�ı���PFCD=S��BCD��������ε�������䣮
��3����B��BM��CD����CD��M����P��PN��EF����EF��N���ɡ�DEQ�ס�BCD����$\frac{DE}{BC}$=$\frac{EQ}{CD}$�����QE���ɡ�PNQ�ס�BMD���� $\frac{PQ}{BD}$=$\frac{PN}{BM}$�����PN������S��PEQ=$\frac{1}{2}$EQ•PN���г�ʽ�Ӽ��ɣ����һ�������з��̽����
��� �⣺��1����PE��ABʱ��
��$\frac{DE}{DA}$=$\frac{DP}{DB}$��
��DE=2t��DP=20-2t��
��$\frac{2t}{12}$=$\frac{20-2t}{20}$��
��t=$\frac{15}{4}$��
�൱t=$\frac{15}{4}$��s����PE��AB��
��2���ڡ�PDE�͡�FBP�У�
��DE=BP=2t��PD=BF=20-2t����PDE=��FBP��
���PDE�ա�FBP��SAS����
��S�����PFCDE=S��PDE+S�ı���PFCD=S��FBP+S�ı���PFCD=S��BCD��
�����˶������У������PFCDE��������䣮
��3����B��BM��CD����CD��M����P��PN��EF����EF��N��
��BC=BD��BM��CD��CD=4cm��
��CM=$\frac{1}{2}$CD=4cm��
��BM=$\sqrt{2{0}^{2}-{4}^{2}}$=8$\sqrt{6}$cm��
��S��BCD=$\frac{1}{2}$CD•BM=$\frac{1}{2}$��8��8$\sqrt{6}$=32$\sqrt{6}$��
���߶�EF��DC������DA���������˶���
��EFƽ���ҵ���CD��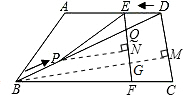
���ı���CDEF��ƽ���ı��Σ�
���DEQ=��C����DQE=��BDC��
��BC=BD=10��
���DEQ�ס�BCD��
��$\frac{DE}{BC}$=$\frac{EQ}{CD}$��
��$\frac{2t}{20}$=$\frac{EQ}{8}$��
��EQ=$\frac{4}{5}$t��
��EF��CD��
���BQF=��BDC����BFG=��BCD��
�֡�BD=BC��
���BDC=��BCD��
���BQF=��BFG��
��ED��BC��
���DEQ=��QFB��
�֡ߡ�EQD=��BQF��
���DEQ=��DQE��
��DE=DQ��
��ED=DQ=BP=2t��
��PQ=20-4t��
�֡ߡ�PNQ�ס�BMD��
��$\frac{PQ}{BD}$=$\frac{PN}{BM}$��
��$\frac{20-4t}{20}$=$\frac{PN}{8\sqrt{6}}$��
��PN=8$\sqrt{6}$��1-$\frac{t}{5}$����
��S��PEQ=$\frac{1}{2}$EQ•PN=$\frac{1}{2}$•$\frac{4}{5}$t•8$\sqrt{6}$��1-$\frac{t}{5}$��=-$\frac{16\sqrt{6}}{25}$t2+$\frac{16\sqrt{6}}{5}$t��
��S��PEQ=$\frac{3}{5}$S��BCD��
����-$\frac{16\sqrt{6}}{25}$t2+$\frac{16\sqrt{6}}{5}$t=$\frac{3}{25}$•32$\sqrt{6}$��
���t1=2��t2=3��
���� ����������ƽ���ߵ����ʣ����������κ�ȫ�������ε��ж������ʣ����ɶ����������ε������ʽ��⣬�ۺ��Խ�ǿ���ѶȽϴ������п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��Ϊ$\frac{1}{2}$ | B�� | ��Ϊ1 | C�� | ��Ϊ$\frac{1}{4}$ | D�� | ��Ϊ$\frac{1}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ax2+bx+c=0 | B�� | x2-bx+c=0 | C�� | ax2+bx=c | D�� | ax2+bx+c=0��a��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����������ABCDEF�ı߳�Ϊ2$\sqrt{3}$���ӳ�BA��EF���ڵ�O����OΪԭ�㣬�Ա�AB���ڵ�ֱ��Ϊx�Ὠ��ƽ��ֱ������ϵ����ֱ��DF��ֱ��EC�Ľ��������ǣ�3$\sqrt{3}$��5����
��ͼ����������ABCDEF�ı߳�Ϊ2$\sqrt{3}$���ӳ�BA��EF���ڵ�O����OΪԭ�㣬�Ա�AB���ڵ�ֱ��Ϊx�Ὠ��ƽ��ֱ������ϵ����ֱ��DF��ֱ��EC�Ľ��������ǣ�3$\sqrt{3}$��5�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ֱ��ǵ����ڵ�һ��Ʒʱ��ʾ��ͼ����֪��������CD�ĸ߶�Ϊ2�ף�֧��BC�ij�Ϊ4�ף���������30��ǣ�����AB��֧��BC�ļн�Ϊ75�㣬����AC������75��ǣ�
��ͼ���ֱ��ǵ����ڵ�һ��Ʒʱ��ʾ��ͼ����֪��������CD�ĸ߶�Ϊ2�ף�֧��BC�ij�Ϊ4�ף���������30��ǣ�����AB��֧��BC�ļн�Ϊ75�㣬����AC������75��ǣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com